2.2 Линейные операции над векторами

Линейными операциями над векторами являются сложение векторов и умножение вектора на число.

Суммой векторов и называется такой вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора приложено к концу вектора (правило треугольника) (рисунок 7).

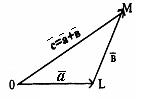
Рисунок 7

При сложении векторов имеют место неравенства:

| + | £ || + ||,

| – | ³ || – ||,

Выражающие, что сторона OM треугольника OML (см. рисунок 7) меньше суммы и больше разности двух других сторон, причем равенство имеет смысл лишь для равнонаправленных векторов в первом неравенстве и для противоположно направленных векторов – во втором неравенстве.

Из определения следует, что сумма двух противоположных векторов равна нуль-вектору

+ (–) = . (2.1)

Сложение векторов подчиняется следующим законам:

А) переместительному закону: + = +;

Б) сочетательному закону: + ( + ) = ( + ) + .

Операция сложения может быть распространена на любое число слагаемых векторов.

Для того чтобы сложить N векторов , надо к концу первого вектора приложить начало второго, затем к концу второго вектора приложить начало третьего и т. д. и, наконец, приложить к концу предпоследнего вектора начало последнего; тогда замыкающий вектор, соединяющий начало первого вектора с концом последнего, и будет являться вектором – суммой данных векторов.

При сложении векторов можно любым образом переставлять и группировать слагаемые.

Вычитание векторов. Разностью векторов и называют вектор , для которого + = . Для геометрического построения вектора–разности можно поступить так: из произвольного начала О строим векторы = , = .

Вектор (проведенный из конца вычитаемого вектора к концу уменьшаемого вектора ) есть разность .

Действительно, сумма равна (рисунок 8).

Рисунок 8

Умножение вектора на скаляр. Произведением вектора на скаляр называется вектор, длина которого равна |l| ||, параллельный и равнонаправленный с , если λ > 0, и противоположно направленный, если λ <0. Обозначается произведение вектора на скаляр λ так: λ или λ. Таким образом, векторы и λ – коллинеарные. Если λ = 0, то, по определению, .

На рисунке 9 показан вектор 2.

Рисунок 9

Если длина вектора равна единице, то вектор называют Ортом. Тогда любой вектор , равнонаправленный вектору , можно представить в виде L, здесь L – длина этого вектора.

Деление вектора на скаляр эквивалентно умножению вектора на число . Умножение вектора на скаляр подчиняется законам: сочетательному l(m) = (lm) и распределительному (l + m) = l + m.

Введем еще одно понятие, важное для дальнейшего. Линейной комбинацией векторов и называется такой вектор , который вычисляется по правилу

. (2.2)

Здесь любые действительные числа.

Аналогично можно ввести понятие линейной комбинации векторов. Вектор называется линейной комбинацией векторов с коэффициентами .

< Предыдущая		Следующая >