3.5.6. Цилиндры второго порядка

В заключение обзора поверхностей второго порядка отметим еще случай, когда в уравнении отсутствует какая-нибудь координата. Такое уравнение определяет Цилиндрическую поверхность второго порядка (или Цилиндр) с образующими, параллельными той оси, координата которой в уравнении отсутствует.

Так, поверхность, заданная уравнением

,

Является цилиндром с образующими, параллельными оси OY. Сечением цилиндра плоскостью XOZ является окружность с центром в начале координат и радиусом, равным единице
(рис. 16). Заметим, что уравнение цилиндра не отличается от уравнения окружности, называемой Направляющей для данного цилиндра.

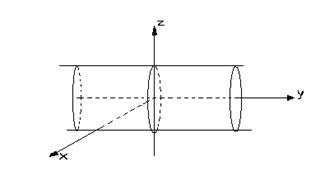
Рис. 16

Среди цилиндров, образующие которых параллельны оси OZ различают цилиндры следующих типов:

А) эллиптический цилиндр

;

При = , получается круговой цилиндр

;

Б) гиперболический цилиндр

;

В) параболические цилиндры

или .

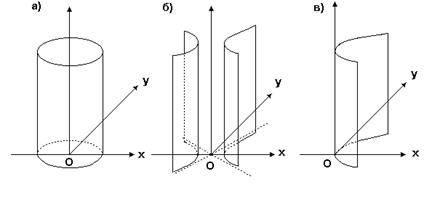
Тип цилиндра зависит от вида направляющей цилиндра в плоскости XOY (рис. 17)

Рис. 17

< Предыдущая		Следующая >