1.2.1. Уравнение плоскости, проходящей через точку M0 (x0,y0,z0) . с данным вектором нормали =(A, B, C)

Перейдем теперь к выводу уравнения плоскости в пространстве. Геометрически плоскость однозначно можно определить различными способами. Например, тремя точками плоскости, не лежащими на одной прямой; парой параллельных прямых и др. Здесь мы рассмотрим плоскость π, проходящую через фиксированную точку M0(x0,y0,z0) и перпендикулярную вектору =(A, B,C), который называется Нормалью К плоскости π, причем , т. е. A2+B2+C2>0 (рис 2).

Вектором нормали к плоскости Ax+By+Cz+D=0 называется ненулевой вектор =(A, B,C), перпендикулярный к данной плоскости.

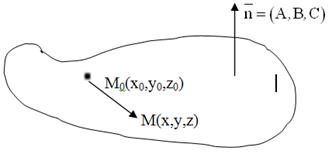
Рис. 2

Пусть M(x, y,z) – текущая точка плоскости (произвольная точка плоскости π). В этом случае вектор лежит на плоскости π и, следовательно, . Воспользуемся условием ортогональности двух векторов

(,)=0 (2)

Распишем уравнение (2) покоординатно:

=(x – x0, y – y0, z – z0), =(A, B,C), отсюда

A(x – x0) + B(y – y0) + C (z – z0)=0 (3)

Уравнение (3) есть уравнение плоскости, проходящей через точку M0 с вектором нормали .

< Предыдущая		Следующая >