Глоссарий
|
№ П/п |
Новое понятие |
Содержание |
|
1 |
Аналитическое представление линии на плоскости |
Уравнение с двумя переменными Х и У |
|
2 |
Асимптоты гиперболы |
Прямые |
|
3 |
Вершина параболы |
Точка пересечения параболы с осью параболы |
|
4 |
Вершины гиперболы |
|
|
5 |
Вершины эллипса |
Точки пересечения эллипса с осями симметрии |
|
6 |
Гипербола |
Геометрическое место точек, разность расстояний которых до двух данных точек F1, F2, называемых фокусами, есть величина постоянная, равна 2A |
|
7 |
Декартовы прямоугольные координаты, определяющие положение точки М на плоскости |
Абсцисса X и ордината Y точки М на плоскости – декартовы прямоугольные координаты |
|
8 |
Задание полярной системы координат |
Задается: точка О – полюс, и ось, проходящая через эту точку – полярная ось |
|
9 |
Каноническое уравнение гиперболы |
|
|
10 |
Каноническое уравнение гиперболы, если ее фокальная ось – ось Y |
|
|
11 |
Каноническое уравнение окружности |
|
|
12 |
Каноническое уравнение параболы |
|
|
13 |
Каноническое уравнение параболы с осью симметрии – осью Y |
|
|
14 |
Каноническое уравнение прямой на плоскости |
|
|
15 |
Каноническое уравнение эллипса |
|
|
16 |
Координаты фокусов гиперболы, если фокальная ось – ось X |
|
|
17 |
Координаты фокусов гиперболы, если фокальная ось – ось Y |
|
|
18 |
Координаты фокусов эллипса, вытянутого вдоль оси X |
|
|
19 |
Координаты фокусов эллипса, вытянутого вдоль оси Y |
|
|
20 |
Начало координат |
Точка пересечения осей координат |
|
21 |
Общее уравнение кривой второго порядка на плоскости |
|
|
22 |
Общее уравнение прямой |
|
|
23 |
Окружность |
Геометрическое место точек, удаленных от точки С (А, B) на равное расстояние R |
|
24 |
Ось симметрии параболы |
Для параболы |
|
25 |
Парабола |
Геометрическое место точек, равноотстоящих от данной точки F, называемой фокусом, и данной прямой, называемой директрисой |
|
26 |
Параметрическое уравнение прямой, проходящей через точку M0(X0,X0) с направляющим вектором |
|
|
27 |
Переход от декартовой системы координат к полярной (полюс и начало координат совпадают) |
|
|
28 |
Переход от полярной системы координат к декартовой (полюс и начало координат в декартовой системе совпадают) |
|
|
29 |
Полярные координаты точки М |
Радиус-вектор R – расстояние точки М от полюса, и полярный угол |
|
30 |
Уравнение директрисы |
|
|
31 |
Уравнение окружности с центром в точке С(A,B) и радиусом R |
|
|
32 |
Уравнение прямой в отрезках (на осях координат). A – прямая отсекает отрезок на оси X, B – на оси Y |
|
|
33 |
Уравнение прямой с угловым коэффициентом |
|
|
34 |
Уравнение прямой, параллельной координатной оси X |
|
|
35 |
Уравнение прямой, параллельной координатной оси Y |
|
|
36 |
Уравнение прямой, проходящей через данную точку M1(X1,X1) с данным угловым коэффициентом K |
|
|
37 |
Уравнение прямой, проходящей через заданные точки M1(X1,X1) и M2(X2,X2) |
|
|
38 |
Условие параллельности двух прямых |
|
|
39 |
Условие перпендикулярности двух прямых |
|
|
40 |
Фокальная ось эллипса |
Ось симметрии, на которой находятся фокусы |
|
41 |
Фокусы параболы |
|
|
42 |
Формула вычисления острого угла q между прямыми |
|
|
43 |
Формула вычисления угла q между двумя прямыми |
|
|
44 |
Формула для вычисления расстояния |
|
|
45 |
Формулы преобразования координат при параллельном переносе (сдвиге) осей |
Координат, (Х, У) – новые координаты точки, (Х, У) – старые координаты точки плоскости |
|
46 |
Центр эллипса |
Точка пересечения осей симметрии |
|
47 |
Эксцентриситет гиперболы |
|
|
48 |
Эксцентриситет эллипса |
Если эллипс вытянут вдоль оси X – |
|
49 |
Эллипс |
Геометрическое место точек, сумма расстояний которых до двух данных точек, F1, F2, называемых фокусами, есть величина постоянная, равна 2A |
| < Предыдущая | Следующая > |
|---|
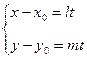 , или
, или 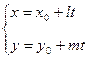 , T – числовой параметр
, T – числовой параметр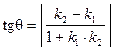
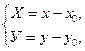 координаты “нового” начала (X0, Y0)
координаты “нового” начала (X0, Y0)