16. Целочисленные задачи линейного программирования

Цели

Нередко приходится рассматривать задачи, в которых неизвест­ные величины могут принимать только целочисленные значения. Например, задачи, связанные с определением необходимого чис­ла рабочих мест или количества дорогостоящих станков. При ре­шении таких задач с целочисленными переменными методы ли­нейного (выпуклого) программирования неприменимы.

Другая сфера применения целочисленных моделей — выбор вариантов. В соответствующих задачах все или некоторые пере­менные могут принимать только два значения: 0 или 1. Такие пе­ременные носят название булевых.

Наиболее известные методы решения целочисленных задач — метод отсечения и метод ветвей и границ. Они разработаны в на­чале 60-х годов XX века и затем неоднократно усовершенствова­лись и модифицировались. Решения примеров и задач, приводи­мых в этой главе, получены с помощью метода ветвей и границ и являются точными.

После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь использовать для экономического анализа следующие понятия:

• неделимость;

• целочисленная задача;

• целочисленная и булева переменные;

• взаимоисключение и взаимообусловленность.

Модели

Дискретные (целочисленные) задачи математического програм­мирования могут возникать различными путями. Существуют за­дачи линейного программирования, которые формально к цело­численным не относятся (требование целочисленности перемен­ных в них в явном виде не накладывается), но которые при целочисленных исходных данных всегда обладают целочисленным планом. Этим свойством обладают транспортная задача и различ­ные ее варианты (задача о назначениях).

Первоначальным стимулом к изучению целочисленных и дис­кретных задач явилось рассмотрение задач линейного программи­рования, в которых переменные представляли физически недели­мые величины (скажем, количество единиц продукции разных видов). Для характеристики этого класса моделей используется термин «задачи с неделимостями».

Другим важным толчком к построению теории дискретного программирования явился новый подход к некоторым экстремаль­ным комбинаторным задачам, для решения которых приходится вводить булевы переменные, носящие логический характер (Х = 1 или Х = 0).

К целочисленным (точнее, частично целочисленным) задачам линейного программирования удается свести также ряд задач, в которых явное требование целочисленности отсутствует, зато имеются некоторые особенности, выводящие их за рамки линей­ного программирования. Эти особенности могут относиться либо к целевой функции, либо к области допустимых решений.

Итак, можно выделить следующие основные классы задач дис­кретного программирования:

1) транспортная задача (см. главу 5) и ее варианты;

2) задачи с неделимостями;

3) экстремальные комбинаторные задачи;

4) задачи с неоднородной разрывной целевой функцией (см. транспортную задачу с фиксированными доплатами в главе 5);

5) задачи на неклассических областях (см. модель оптимального размера заказа с количественными скидками в главе 12).

Целочисленная задача линейного программирования (задача с неделимостями). К данному классу принадлежат Задачи распре­деления капиталовложении и Задачи планирования производства.

Целочисленная задача линейного программирования заключа­ется в максимизации функции:

(1)

При условиях

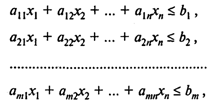(2)

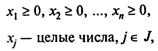
Где J — некоторое подмножество множества индексов N = ={1,2,...,N}.

Если J = N (T. e. требование целочисленности наложено на все переменные), то задачу называют Полностью целочисленной; если же J ¹ N, она называется Частично целочисленной.

Модель (1)—(4) естественно интерпретировать, например, в следующих терминах. Пусть через I = 1,..., Т обозначены произ­водственные факторы, через J = 1, ..., П — виды конечной про­дукции.

Обозначим далее:

Aij — количество факторов I, необходимое для производства единицы продукта J;

Bi — наличные ресурсы фактора I;

СI — прибыль, получаемая от единицы продукта J.

Пусть продукты J для JÎJ являются неделимыми, т. е. физи­ческий смысл имеет лишь их целое неотрицательное количество («штуки»). Предположим, что требуется составить производствен­ную программу, обеспечивающую максимум суммарной прибы­ли и не выводящую за пределы данных ресурсов. Обозначая через Xj искомые объемы выпуска продукции, мы сводим эту задачу к мо­дели (1)-(4).

Задача с булевыми переменными. Логическая взаимосвязь:

1) Взаимоисключение. Пусть Xj = 1, если реализуется проект АJ, И ХJ = 0 в противном случае. Запись AjÚAk означает, что в план может быть включен либо проект АJ, либо проект АK. Вместе они включены быть не могут. С помощью этой записи выражается от­ношение взаимоисключения между проектами.

В этих обозначениях взаимоисключение Aj Ú АK выражается неравенством ХJ + ХK £ 1;

2) Взаимообусловленность. Запись АK ® Aj («проект АK влечет за собой проект АJ») означает, что проект АK может быть включен в план только в том случае, если в план включен и проект Aj. С по­мощью этой записи выражается отношение между обусловлива­ющими друг друга проектами, например когда проект Ak — резуль­тат тиражирования проекта Aj на другом объекте или когда АK ба­зируется на результатах реализации проекта Aj.

В принятых обозначениях взаимообусловленность АK ® АJ вы­ражается неравенством ХK £ ХJ.

Экстремальные комбинаторные задачи. Задачи данного класса, называемые также задачами выбора, состоят в отыскании среди конечного множества альтернатив одной, которой отвечает экст­ремальное значение принятой целевой функции.

Задача о коммивояжере — классический пример задачи выбора оптимального маршрута. Формулируется она следующим образом. Коммивояжер должен выехать из определенного города и вернуть­ся в него, побывав в каждом из городов лишь по одному разу и проехав минимальное расстояние.

Пусть ХIj = 1, если коммивояжер переезжает из города I непо­средственно в город J, и Xij = 0 в противном случае. Обозначим через СIj расстояние между городами I и J (чтобы избежать бессмыс­ленных значений ХIj = 1, предполагается, что СIi равны достаточно большому числу).

Тогда формальная модель имеет вид

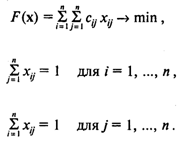
К приведенным ограничениям необходимо добавить условия на недопустимость подциклов, т. е. повторного посещения горо­дов (за исключением исходного). Это ограничения вида

Где на переменные Zi и Zj не требуется накладывать никаких огра­ничений.

Общая Задача календарного планирования формулируется следу­ющим образом. Имеется П станков (машин), на которых требует­ся обработать M деталей. Заданы маршруты (в общем случае раз­личные) обработки каждой детали на каждом из станков или груп­пе станков. Задана также продолжительность операций обработки деталей. Предполагается, что одновременно на станке можно об­рабатывать не более одной детали. Требуется определить опти­мальную последовательность обработки. Критерием оптимально­сти могут выступать продолжительность обработки всех деталей, суммарные затраты на обработку, общее время простоя станков и др. Существует огромное число постановок данной задачи, учи­тывающих конкретные условия производства.

Один из представителей задач данного типа — так называемая Задача о ранце. Имеется П предметов. Предмет J (J = 1, ..., П) об­ладает весом Wj и полезностью СJ. Пусть B — общий максимально допустимый вес предметов, которые можно положить в ранец. Требуется выбрать предметы таким образом, чтобы их общий вес не превышал максимально допустимый и при этом суммарная по­лезность (ценность) содержимого ранца была максимальной. Пусть ХJ = 1, если предмет положен в ранец, и ХJ = 0 в противном случае. Математическая формулировка задачи имеет вид

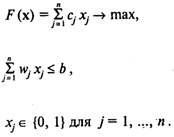
К классу экстремальных комбинаторных задач принадлежит также линейный и нелинейный варианты Задача о назначениях (ли­нейный вариант такой задачи рассмотрен в главе 6).

Большинство целочисленных и комбинаторных типов задач, таких, как задача с неделимостями, задача коммивояжера, задача календарного планирования, принадлежит к разряду так называ­емых Трудно решаемых. Это означает, что вычислительная слож­ность алгоритма их точного решения — зависимость числа элемен­тарных операций (операций сложения или сравнения), необходи­мых для получения точного решения, от размерности задачи я — является Экспоненциальной (порядка 2N), т. е. сравнимой по тру­доемкости с полным перебором вариантов. В качестве П, например, для задачи с неделимостями служит число целочисленных перемен­ных и число ограничений, для задачи коммивояжера — число горо­дов (или узлов графа маршрутов), для задачи календарного плани­рования — число деталей и число станков. Такие задачи называют еще NP-трудными или NP-Полными. Получение их точного ре­шения не может быть гарантировано, хотя для некоторых задач данного типа существуют эффективные методы, позволяющие находить точное решение даже при больших размерностях. Примером таких задач служит задача о ранце с булевыми пере­менными.

Задачи с вычислительной сложностью, определяемой Полино­миальной зависимостью от П, называются Эффективно решаемы­ми. К такого типа задачам принадлежат задачи транспортного типа и линейные задачи о назначениях.

Для решения целочисленных задач используются следующие методы:

1) симплекс-метод (для транспортных задач, задач о назначениях);

2) метод отсечения (метод Гомори);

3) метод ветвей и границ (в общем случае не обеспечивает получения точного решения);

4) эвристические методы (не обеспечивают получения точно­го решения).

Последняя группа методов может использоваться в случаях, когда применение предыдущих методов невозможно или не при­водит к успеху. Кроме того, эвристические методы можно исполь­зовать для решения задач любой сложности.

< Предыдущая		Следующая >