16.1. Примеры

Пример 1. Оптимизация капиталовложений.

Имеется 10 работ (А1 ¸ А2), каждая из которых характеризуется тремя технико-экономическими показателями:

АJ — трудозатраты;

Bj — размер, необходимых капиталовложений;

СJ — ожидаемый экономический эффект.

Исходные данные приведены в следующей таблице:

Общие трудозатраты не должны превышать 20. Общий объем капиталовложений не должен превышать 20. Определите, какие из 10 работ следует выполнить, чтобы максимизировать ожида­емый экономический эффект, учитывая следующие условия вза­имообусловленности и взаимоисключения:

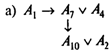
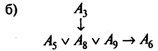
Решение. Помимо целевой функции и двух ограничений по общему объему трудозатрат и капиталовложений, данную задачу характеризует следующая система неравенств:

В результате расчетов получаем Х* = (0101110010).

Пример 2. Оптимизация производственной программы.

Автомобилестроительный завод выпускает три модели автомо­билей, которые изготавливаются последовательно в трех цехах. Мощность цехов составляет 300, 250 и 200 человекодней в дека­ду. В первом цехе для сборки одного автомобиля первой модели требуется б человекодней, второй модели — 4 и третьей модели — 2 человекодня в декаду соответственно. Во втором цехе трудоем­кость равна 3,4 и 5 человекодней соответственно, в третьем — по 3 человекодня на каждую модель. Прибыль, получаемая заводом от продажи одного автомобиля каждой модели, составляет соот­ветственно 15, 13 и 10 тыс. долл.

Постройте модель для определения оптимального плана.

Решение. Пусть ХI — количество выпускаемых автомобилей I-Й модели в течение декады (I = 1,..., N). В принятых обозначе­ниях модель имеет вид

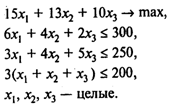
Пример 3. Двумерная задача раскроя.

Из минимального количества листов стекла размером 8 х 6 м2 требуется вырезать 10 оконных стекол размером 4 х 4 м2, 20 окон­ных стекол размером 4 х 5 м2 и 30 оконных стекол размером 3х3 м2. Множество вариантов раскроя (см. главу 3) показано в следующей таблице:

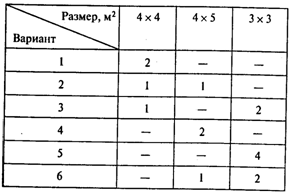
Построите модель для определения плана раскроя, требующе­го минимального количества материала.

Решение. Пусть ХI — количество листов стекла размером 8 х 6 м2, которые следует раскроить по варианту I.

Тогда модель имеет вид

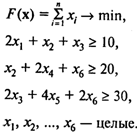
Пример 4. Задача о ранце.

Некая торговая компания имеет свои универсамы в Москве, Санкт-Петербурге, Нижнем Новгороде, Екатеринбурге, Самаре, Воронеже и Казани. В результате ошибок менеджмента экономи­ческое положение компании стало ухудшаться, ей пришлось взять кредит в размере 13 млн руб. и в конечном счете, чтобы вовремя его погасить, срочно продавать некоторые из своих универсамов. Средства, которые компания могла бы получить от продажи уни­версамов в Москве, Санкт-Петербурге, Нижнем Новгороде, Ека­теринбурге, Самаре, Воронеже или Казани, составляют соответ­ственно 5,2; 4,9; 4,5; 3,6; 3,4; 3,2 и 3,1 млн руб. Однако продажа универсамов сопряжена с необходимостью увольнения персона­ла. Его численность составляет соответственно 200,190,180,170, 150,130 и 110 человек. По требованию объединенного профсоюза работников торговли компания должна минимизировать числен­ность увольняемого персонала.

Постройте модель для нахождения оптимального решения.

Решение. Пронумеруем города в соответствии с порядком их перечисления. Пусть ХI = 1, если универсам, расположенный в го­роде, продается, и ХI = 0 в противном случае. Тогда оптимизаци­онная модель имеет вид

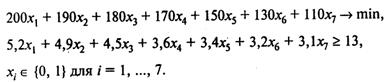
< Предыдущая		Следующая >