14.4. Ситуации
Ситуация 1. Супермаркет «Север».
«Север» — недавно открытый супермаркет в Северном административном округе Москвы, где существует большая конкуренция между подобными магазинами. Новый управляющий Петр Перфилов понимает, что при высокой конкуренции покупатели скорее пойдут туда, где им предложат лучшее обслуживание и более широкий ассортимент товаров. Он гордится своим магазином, большим выбором различных сортов мяса и сыра, а также мясным прилавком, где покупатель может попробовать нарезки мяса и птицы.
Петр уверен, что быстрое и эффективное обслуживание может привлечь покупателей и повысить конкурентоспособность. Он ввел систему безналичных расчетов за покупки и внедрил службу «Доставка на дом», чтобы сделать приобретение покупок более удобным, особенно для пожилых горожан. Следующий этап — установка новых кассовых аппаратов, недавно появившихся в сфере обслуживания. Основной вопрос: сколько аппаратов следует установить? Слишком много — нежелательно. Но не потому, что появятся дополнительные издержки. Более важный аспект — эффективное использование площадей.
Планируя новый дизайн системы контроля, Петр собрал данные о нескольких последовательных субботних, наиболее посещаемых, утренних часах в своем магазине. Он заметил, что покупатели прибывают на контроль приблизительно по 10 человек в час. 20% покупателей оплачивают 10 или менее наименований продуктов, и в среднем их обслуживают в течение 2 мин, в то время как на покупателей с более чем 10 товарами кассир затрачивает по 4 мин.
Задание
Помогите Петру определить, сколько новых кассовых аппаратов следует установить.
Ответы и решения
Ответы на вопросы: 1—4, 2 — 3, 3—2, 4—4, 5—2, 6—1.
Задача 1. Решение.
Рассматриваем Модель А.
Среднее число клиентов в очереди
![]()
Среднее число клиентов в системе
![]()
Среднее время ожидания
![]()
Среднее время, которое клиент проводит в системе,
![]()
В среднем за 5 мин прибывают (24 : 60) • 5 = 2 клиента.
Вероятности того, что 0, 1, 2, 3 клиента прибудут за 5 мин, найдем по формуле, описывающей вероятность поступления заявок в систему (т. е. по закону Пуассона):

Вероятность того, что в течение 5 мин прибудут более 3 клиентов, равна 1 - [Р(0) +р(1) +р(2) +р(3)] = 1 – (0,135 + 0,27 + 0,27 + 0,18) = 0,145.
Вероятность того, что фактическое время обслуживания заявки T не превысит заданной величины t, подчинена экспоненциальному закону и может быть определена по формуле Р(T < t) = 1 – e–tm, где средний темп обслуживания m = 0,6 клиента в минуту:
А) вероятность того, что время обслуживания не превысит 1 мин, Р(T < 1) = 1 – e–0,6×1 = 0,45;
Б) вероятность того, что время обслуживания не превысит 2 мин, Р(T < 2) = 1 – e–0,6×2 = 0,70;
В) вероятность того, что время обслуживания составит более 2 мин, равна 1 – Р(T < 2) = 0,30.
Вероятность того, что прибывающему клиенту придется ждать обслуживания,
![]()
Вероятность того, что в системе находится П клиентов, можно найти, используя предельные вероятности одноканальной системы с неограниченной очередью:
А) 0 клиентов:
![]()
Б) 3 клиента: P3 = R3•Р0 = (0,667)3•0,33 = 0,098;
В) более 3 клиентов: ![]()
Ответы: 1. Два клиента. 2. 0,135; 0,27; 0,27; 0,18.
3. 0,145. 4. а) 0,45; 6) 0,7; в) 0,3.
5. 0,067. 6. а) 0,33; 6) 0,098; в) 0,198.
Задача 2. Решение.
Используем пакет POMWIN. Заполним модель М/М/1 исходными данными.
Для первого механика l = 2 клиента в час, m = 3 клиента в час, СМех = 7 долл /ч; СОж =15долл./ч:

Среднее время, которое клиент проводит в очереди, Wq = 0,667 ч;
Средняя длина очереди LQ = 1,333;
Среднее время, которое клиент проводит в системе обслуживания, WS = 1 ч;
Среднее число клиентов в системе обслуживания LS = 2;
Вероятность того, что система обслуживания окажется свободной, равна 1 – R = 1 – 0,667 = 0,333.
Совокупные издержки по ожиданию в очереди и оплате первому механику равны 27 долл. в час.
Для второго механика l = 2 клиента в час, m = 4 клиента в час, Смех = 10 долл./ч, Сож = 15долл./ч:
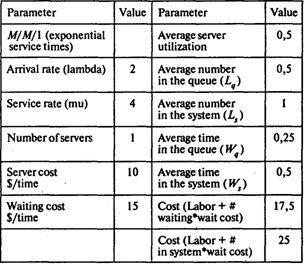
Среднее время, которое клиент проводит в очереди, Wq = 0,25 ч;
Средняя длина очереди Lq = 0,5;
Среднее время, которое клиент проводит в системе обслуживания, WS = 0,5 ч;
Среднее число клиентов в системе обслуживания LS = 1;
Вероятность того, что система обслуживания окажется незанятой равна 1–R = 1–0,5 = 0,5.
Совокупные издержки по ожиданию в очереди и оплате второму механику равны 17,5 долл. в час.
По результатам расчетов можно сделать вывод, что следует нанять второго механика.
Ответы: 1. Второго механика. 2. 17,5 долл./ч.
Задача 3. Решение.
Заполним модель М/М/1 с одним продавцом (он же является кассиром) (l = 15 покупателей в час, m = 20 покупателей в час):

Среднее время, которое покупатель проводит в очереди, WQ = 0,15 ч = 9 мин;
Средняя длина очереди LQ = 2,25;
Среднее время, которое покупатель проводит в магазине Ws = 0,2 ч = 12 мин;
Среднее число покупателей в магазине LS = 3;
Вероятность того, что в магазине не окажется покупателей, Р0 = 1 – R = 1 – 0,75 = 0,25.
Если нанять продавца, который бы выполнял заказ, в то время как кассир рассчитывается с покупателем (альтернатива А), увеличится темп обслуживания клиентов (m = 30 покупателей в час), система останется одноканальной. Используем для решения этой задачи модель М/М/1:

Среднее время, которое покупатель проводит в очереди, в этом случае сократилось до WQ = 2 мин, издержки по ожиданию в очереди и обслуживанию канала сократились до 7 долл. в час.
Если нанять второго кассира, тем самым создав в магазине двухканальную очередь (альтернатива В), темп обслуживания на каждом канале будет равен m = 20 покупателей в час. Используем для решения этой задачи модель M/M/S:
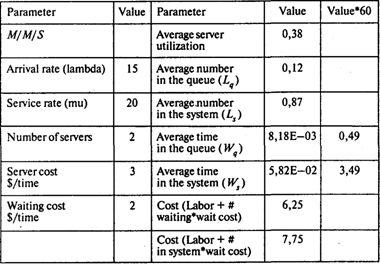
Среднее время, которое покупатель проводит в очереди, в этом случае сократилось до WQ = 0,49 мин, издержки сократились до 6,25 долл. в час. Последний вариант более экономичен.
Ответ: Альтернативу В.
Задача 4. Решение. Заполним модель М/М/1:

Вероятность того, что док будет пуст, Р0 = 1 – 0,5 = 0,5;
Среднее число судов в очереди Lq = 0,5;
Среднее время ожидания обслуживания Wq = 0,1 ч = 6 мин;
Среднее время пребывания в доке Ws = 0,2 ч = 12 мин.
Построим двухканальную систему обслуживания:
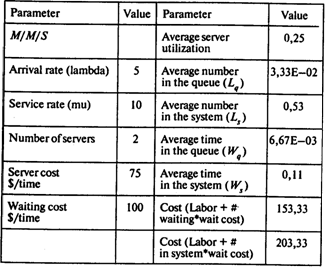
Степень загрузки системы сократилась до 0,25, совокупные издержки увеличились на 28 долл. в час (203 - 175 = 28). Необходимости в строительстве второго дока нет.
Ответы: 1. 0,5. 2. 0,5 судна. 3. 6 мин. 4. 12 мин. 5. Нет необходимости.
Задача 5. Решение. Используем модель M/M/1:

Если приобрести второй кассовый аппарат, создав в магазине двухканальную очередь, издержки сокращаются на 4,38 долл. в час (8,75 — 4,37 = 4,38):

Включение третьего кассового аппарата ведет к увеличению издержек, поэтому нет необходимости в его приобретении:

Ответы: 1. Да, есть. 2. Нет необходимости.
Задача 6. Решение.
А. Заполним модель М/М/1 (l = 24 машины в час, m = 60/2 = 30 машин в час); одновременно заполним издержки по обслуживанию канала, включая оплату служащего, и издержки по простою клиентов в очереди:

Вероятность того, что в системе нет машин, Р0 = 1 – 0,8 = 0,2;
Среднее число машин в очереди Lq = 3,2;
Среднее время ожидания обслуживания Wq = 8 мин;
Среднее время пребывания в системе Ws = 10 мин;
Среднее число машин в системе Ls = 4;
Вероятность того, что вновь прибывшей машине придется ждать, РN>0 = 0,8.
В. Используем модель М/М/1 (l = 24 машины в час, m = 60/1,25 = 48 машин в час):
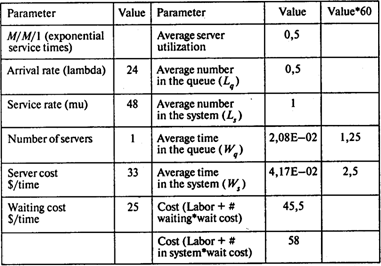
Вероятность того, что в системе нет машин, Р0 = 1 – 0,5 = 0,5;
Среднее число машин в очереди LQ = 0,5;
Среднее время ожидания обслуживания Wq =1,25 мин;
Среднее время пребывания в системе Ws = 2,5 мин;
Среднее число машин в системе Ls= 1;
Вероятность того, что вновь прибывшей машине придется ждать, РN>0 = 0,5.
С. Используем модель M/M/S (l = 24 машины в час, m = 60/2 = 30 машин в час):

Окончание таблицы

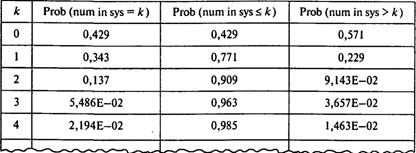
Вероятность того, что в системе нет машин, Р0 = 0,43;
Среднее число машин в очереди Lq = 0,15;
Среднее время ожидания обслуживания WQ = 0,381 мин;
Среднее время пребывания в системе Ws = 2,381 мин;
Среднее число машин в системе LS = 0,95;
Вероятность того, что вновь прибывшей машине придется ждать, РN>0 = 0,57.
Часовые издержки по обслуживанию каналов и простою клиентов в очереди в первом случае составляют 106,5 долл., во втором — 45,5 долл., в третьем — 56,81 долл. Можно сделать вывод, что вариант B для фирмы требует меньших затрат.
Ответ: Вариант В.
Задача 7. Решение.
При использовании одноканальной модели каждый механик находится в системе 4 мин. Определим темп обслуживания клиентов m, если ![]() = 4 мин и l = 4 клиента в минуту. Темп обслуживания для одноканальной системы равен m = 4,25 клиента в минуту:
= 4 мин и l = 4 клиента в минуту. Темп обслуживания для одноканальной системы равен m = 4,25 клиента в минуту:
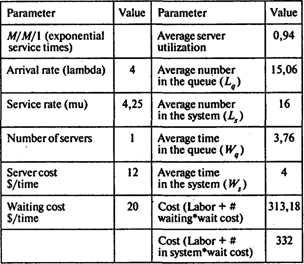
Среднее число клиентов в системе LS = 16;
Среднее время обслуживания одного клиента в системе равно Ws – Wq = 0,23 мин;
Среднее число клиентов в очереди Lq = 15,06.
Построим двухканальную систему:

Среднее число клиентов в системе LS = 1,2;
Среднее время обслуживания одного клиента в системе равно Ws – Wq = 0,23 мин;
Среднее число клиентов в очереди Lq = 0,27.
В одноканальной модели издержки по ожиданию и обслуживанию выше издержек двухканальной модели на 283,83 руб. в минуту (313,18 — 29,35 = 283,83).
Ответ: Двухканальная система.
Задача 8. Решение.
Используем модель M/D/1:

Среднее число автомобилей в очереди Lq = 0,064;
Среднее время ожидания Wq = 1,28 мин;
В течение 30% рабочего времени система занята.
Ответы: 1. 0,064 автомобиля. 2. 1,28 мин. 3. 30% рабочего времени.
Задача 9. Решение.
Заполним модель M/M/S для случая работы одного механика:
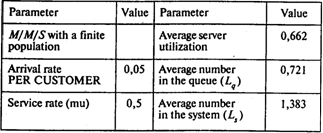
Окончание таблицы


Вероятность того, что все машины работают и механик простаивает, Р0 = 0,338;
Среднее число ожидающих ремонта машин Lq = 0,721;
Среднее число машин в системе Ls = 1,383;
Среднее время ожидания начала ремонта Wq = 2,18 ч;
Среднее время нахождения в системе (ожидание и ремонт) Ws = 4,181 ч.
Если нанять второго механика, получим
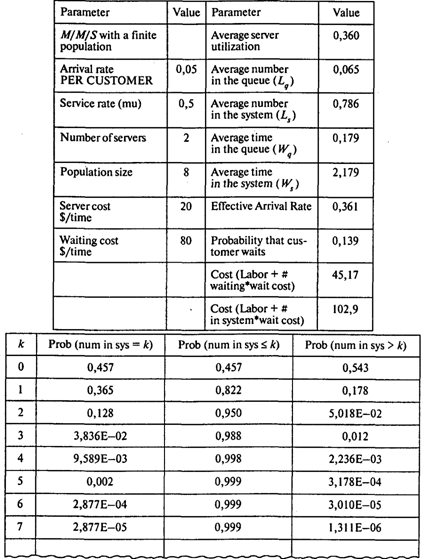
Вероятность того, что все машины работают и механик простаивает, Р0 = 0,457;
Среднее число ожидающих ремонта машин Lq = 0,065;
Среднее число машин в системе LQ = 0,786;
Среднее время ожидания начала ремонта WQ = 0,179 ч;
Среднее время нахождения в системе (ожидание и ремонт) Ws = 2,179 ч.
С экономической точки зрения выгоднее нанять двух механиков.
Ответ: Двух механиков.
Задача 10. Решение.
Используем модель с ограниченной популяцией:

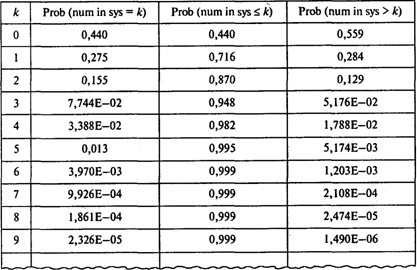
Вероятность того, что ни один грузовик не ожидает погрузки-разгрузки, Р0 = 0,44;
Среднее число грузовиков в очереди Lq = 0,490;
Среднее число грузовиков у магазина LS = 1,049;
Среднее время ожидания Wq = 0,219 ч = 13 мин;
Издержки по функционированию системы равны 54,48 долл. в час.
Ответ: 54,48 долл.
| < Предыдущая | Следующая > |
|---|