12.3. Задачи
Задача 1. Компания «Комуойл» производит на одном из своих заводов три марки неэтилированного бензина А-88, А-92 и А-95 из нефти, добываемой на трех месторождениях: на двух сибирских — тюменском и самотлорском — и на башкирском. Причем из Сибири нефть поступает по трубопроводу в смеси в количестве 250 т в сутки.
Данные о нефти представлены в следующей таблице:

Требуемые характеристики бензина:
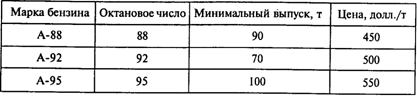
Предположим, что других затрат, кроме затрат на покупку сырой нефти, нет. Определите оптимальную (с точки зрения максимума прибыли) суточную производственную программу завода.
Вопросы:
1. Какова максимальная прибыль завода?
2. Каков оптимальный выпуск бензина А-88?
3. Какова доля тюменской нефти в смеси, поступающей из Сибири?
4. Каковы общие затраты?
Задача 2. На кондитерской фабрике «Десерт» вследствие уменьшения спроса на ряд ее изделий освободилась часть производственных мощностей. Чтобы избежать сокращения численности работающих, специалисты фабрики разработали технологию производства двух новых видов шоколадных конфет: шоколадных бочонков с коньяком, получивших название «Братец Иванушка» (БИ), и шоколадных шариков с вишней, названных «Сестрица Аленушка» (СА). Для изготовления любого нового вида конфет должны быть задействованы три производственные линии: производство шоколада, непосредственное изготовление конфет, упаковка и контроль. Первая и третья линии — общие для конфет обоих наименований. Доля шоколада в общем весе одной конфеты БИ составляет 70%, а в конфете СА — 80%. Максимальная мощность линии по изготовлению шоколада (для новой продукции) составляет 250 кг в сутки. Производительность линии по изготовлению конфет БИ — 170 кг в сутки, конфет СА — также 170 кг. Удельные переменные затраты составляют: для конфет БИ — 180 руб./кг, для конфет СА — 150 руб./кг. Предполагается, что все изготовленные в течение суток конфеты будут проданы. В силу своей исключительности новые изделия не испытывают внешней конкуренции, однако они конкурируют друг с другом. В результате проведенного исследования были получены следующие зависимости объемов сбыта от цен:
![]()
Где X1 — произведенное (проданное) в течение суток количество конфет БИ, кг;
Х2 — произведенное (проданное) в течение суток количество конфет СА, кг;
Р1 — цена конфет БИ, руб./кг;
Р2 — цена конфет СА, руб./кг.
Определите производственную программу, при которой суточная прибыль фабрики от производства новой продукции максимальна.
Вопросы:
1. Какова максимальная прибыль фабрики?
2. Каков оптимальный выпуск конфет БИ?
3. Каков оптимальный выпуск конфет СА?
4. Какова оптимальная цена конфет БИ?
5. Какова оптимальная цена конфет СА?
Задача 3. На молочном комбинате помимо других продуктов производится также сырковая масса трех наименований: «Изюминка», «Ваниль» и «Орешек» — жирности соответственно 6, 5 и 3%. В качестве основных исходных продуктов используются творог жирности 8, 7 и 2%, объемы суточных поставок которого составляют по 200 кг каждого вида, и сахар, имеющийся в количестве 70 кг в сутки.
По технологии для получения 1 кг сырковой массы «Изюминка» требуется 30 г сахара, для «Ванили» — 40 г и для «Орешка» — 60 г. Цена сырковой массы «Изюминка» равна 36 руб./кг, «Ванили» — 35 руб./кг, «Орешка» — 33 руб./кг.
Закупочная цена творога 8%-й жирности определяется зависимостью (29 – 0,003X) руб./кг, где Х — объем закупки (в кг). Аналогичные зависимости для творога 7%-й жирности (27 – 0,008X) руб./кг и 2%-й жирности (26 – 0,005X) руб./кг.
Минимальный выпуск для «Изюминки» 100 кг, «Ванили» 50 кг, «Орешка» 50 кг.
Постройте производственную программу, максимизирующую общую суточную прибыль.
Вопросы:
1. Какова максимальная прибыль?
2. Каков оптимальный объем производства сырковой массы «Орешек»?
3. Каков оптимальный объем производства сырковой массы «Ваниль»?
Задача 4. Горно-обогатительная фабрика получает из руды, поступающей из двух месторождений, никель, медь и серебро. Данные о количестве ценных металлов, получаемых из одной тонны руды каждого месторождения, приведены в следующей таблице:
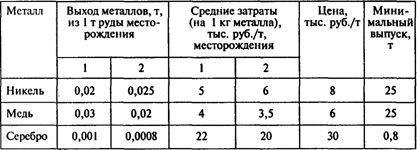
В течение месяца фабрика перерабатывает не более 1000 т руды. За счет увеличения (уменьшения) затрат можно изменить доли выхода металлов в пределах ±10% по сравнению с приведенными в таблице. Предположим, что удельные затраты после изменения средних (приведенных в таблице) коэффициентов выхода металлов определяются зависимостью с = (2K – 1) с0, где K показывает, во сколько раз изменяется средний выход металла из 1 т руды, а с0 — средние удельные затраты. При этом предполагается, что общие затраты, связанные с изменением нескольких коэффициентов, аддитивны.
Постройте модель нелинейного программирования с учетом возможности изменения коэффициентов выхода металлов. Определите оптимальные значения коэффициентов, обеспечивающих максимум прибыли фабрики.
Вопросы:
1. Какова максимальная прибыль?
2. Каково оптимальное значение коэффициента выхода никеля из руды месторождения 2?
3. Каково оптимальное значение коэффициента выхода меди из руды месторождения 1?
4. Какое количество руды месторождения 2 следует использовать в производстве?
Задача 5. Завод производит два вида высококачественного паркета из дуба, отличающиеся формой и толщиной деталей. Дефицитными ресурсами служат дубовая доска и специальная жидкость для пропитки деталей. Для производства 1 м2 паркета первого вида требуется 0,01 м3 дубовой доски и 0,05 кг жидкости для пропитки. Для производства 1 м2 паркета второго вида потребности в ресурсах составляют соответственно 0,02 м3 и 0,15 кг. Максимальное количество ресурсов за месяц: 20 м3 дубовой доски и 150 кг жидкости для пропитки.
Затраты на единицу первого ресурса (на 1 м3 дубовой доски) составляют (1000 – 3R1) руб./м3, где R1 — объем дубовых досок, использованных в производстве паркета. Затраты на единицу второго ресурса (на 1 кг жидкости для пропитки) составляют (500 – 0,5R2) руб./кг, где R2 — количество использованной в производстве паркета жидкости для пропитки. Предполагается, что других затрат нет. Оба вида паркета могут частично заменять друг друга, поэтому величины спроса на них взаимозависимы. Цена 1 м2 паркета первого вида (руб./м2) определяется зависимостью P1 = 100 – 0,04X1 — 0,01X2, а цена 1 м2 паркета второго вида — зависимостью P2 = 210 – 0,008X1 – 0,03X2, где X1, Х2 — объемы производства (м2) паркета соответственно первого и второго вида.
В предположении, что весь паркет может быть продан, определите производственную программу завода, обеспечивающую максимум прибыли.
Вопросы:
1. Какова максимальная прибыль предприятия?
2. По какой цене следует продавать паркет первого вида?
3. По какой цене следует продавать паркет второго вида?
4. Какое количество жидкости для пропитки используется в производстве?
5. Каков оптимальный выпуск паркета второго вида?
Задача 6. Данная задача является одним из вариантов задачи формирования портфеля ценных бумаг (см. пример 2).
Клиент поручил брокерской конторе купить для него на 3 млн руб. акции четырех известных ему компаний. Сделка заключается на год. Клиент заинтересован в минимальном риске при условии, чтобы средний процент прибыли, обеспечиваемый портфелем акций к концу года, был не менее 9%. Известно, что средние значения процентов годовой прибыли от акций компаний составляют соответственно 8,5; 13; 9 и 10%.
Дисперсии процентов прибыли: s11 = 0,1, s22 = 0,19, s33 = 0,13, s44 = 0,14.
Ковариации: s12 = 0,05, s13 = 0,02, s14 = 0,03, s23 = 0,04, s24 = 0,03, s34 = 0,01.
Вопросы:
1. Чему равна средняя годовая прибыль?
2. На какую сумму следует купить акции компании 1?
3. На какую сумму следует купить акции компании 2?
4. Какова минимальная дисперсия портфеля акций?
Ответы и решения
Ответы на вопросы: 1—4, 2 — 1, 3—4, 4 — 5, 5—2, 6—5, 7—4, 8—2, 9—4, 10—2.
Задача 1. Решение.
Введем обозначения:

(Количество нефти измеряется в килограммах.)
В данных обозначениях оптимизационная модель нелинейного программирования имеет вид


Все переменные неотрицательны.
Модель и результаты решения в представлении программы GINO имеют вид

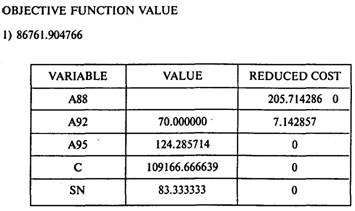
Окончание таблицы
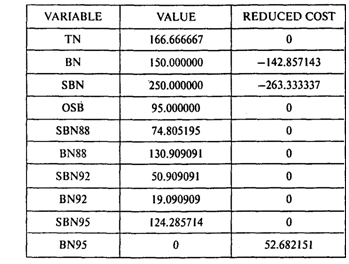
Ответы: 1.86 761,9 долл. 2.205,7т. 3.0,66. 4.109 167 долл.
Задача 2. Решение.
Модель имеет вид

Модель и результаты решения в представлении программы GINO имеют вид

Получаем следующее решение:
OBJECTIVE FUNCTION VALUE
1) 93003.779091

Ответы: 1. 93 тыс. руб. 2. 163 кг. 3. 170 кг. 4. 429 руб. 5. 459 руб.
Задача 3. Решение.
Введем обозначения:

(Количество сырковой массы и творога измеряется в килограммах.)
В указанных обозначениях модель имеет вид

![]()
![]()
Все переменные неотрицательны.
Модель и результаты решения в представлении программы GINO имеют вид

Получаем следующее решение:
OBJECTIVE FUNCTION VALUE
1) 6175.062247

Ответы: 1. 6175 руб. 2. 50 кг. 3. 61,5 кг.
Задача 4. Решение.
Введем обозначения:

Выручка от переработки руды первого месторождения:
![]()
Выручка от переработки руды второго месторождения:
![]()
Затраты, связанные с использованием руды первого месторождения:
![]()
Затраты, связанные с использованием руды второго месторождения:
![]()
Прибыль, получаемая в результате переработки руды первого месторождения:
![]()
Прибыль, получаемая в результате переработки руды второго месторождения:
![]()
Модель нелинейного программирования имеет вид
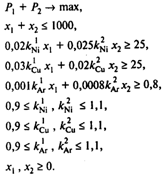
Модель и результаты решения в представлении программы GINO имеют вид



Получаем следующее решение:
OBJECTIVE FUNCTION VALUE
1) 95.109092
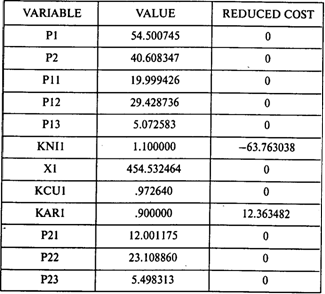
Окончание таблицы
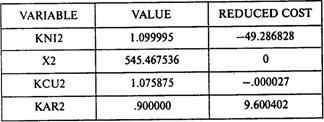
Ответы: 1. 95,1 тыс. руб. 2. 1,1. 3. 0,973. 4. 545,5 т.
Задача 5. Решение.
Модель и результаты решения в представлении программы GINO имеют вид

Получаем следующее решение:
OBJECTIVE FUNCTION VALUE
1) 99073.977899

Ответы: 1. 99 074 руб. 2. 82,78 руб./м2. 3. 181.44 руб./м2. 4. 144,84 кг. 5. 897 м2.
Задача 6. Решение.
Пусть Xj — объем средств, затраченных на покупку акций типа J (тыс. руб.), sIj = SJi, для I ¹ J. В указанных обозначениях модель имеет вид

Модель и результаты решения в представлении программы GINO имеют вид
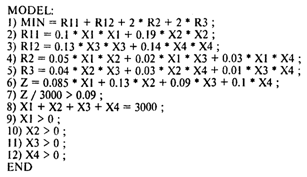
Получаем следующее решение:
OBJECTIVE FUNCTION VALUE
1) 475780.187947
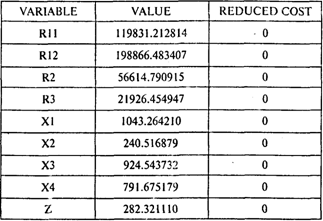
Ответы: 1. 282 тыс. руб. 2. 1043 тыс. руб. 3. 240 тыс. руб. 4. 475 780.
| < Предыдущая | Следующая > |
|---|