12.2. Вопросы
Вопрос 1. Дана действительная функция F(Х), определенная на отрезке действительных чисел S = [0, 100]. Пусть Х1 и Х2 — точки этого отрезка и 0 £ l £ 1.
Какое из нижеприведенных неравенств является условием выпуклости функции?
Варианты ответов:

Вопрос 2. Дана действительная функция F(X), определенная на отрезке действительных чисел S=[0, 100]. Пусть X1 и X2 — точки этого отрезка и 0 £ l £ 1.
Какое из нижеприведенных неравенств является условием строгой вогнутости функции?
Варианты ответов:
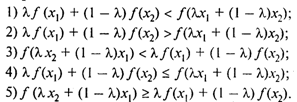
Вопрос 3. Функция ![]()
1) выпуклая;
2) строго выпуклая;
3) вогнутая;
4) строго вогнутая;
5) выпуклая и вогнутая.
Вопрос 4. Функция ![]()
1) выпуклая;
2) ни выпуклая, ни вогнутая;
3) вогнутая;
4) строго вогнутая;
5) выпуклая и вогнутая.
Вопрос 5. Функция ![]() всюду:
всюду:
1) выпуклая;
2) ни выпуклая, ни вогнутая;
3) строго выпуклая;
4) вогнутая:
5) выпуклая и вогнутая.
Вопрос 6. Новая модель скоростного мотоцикла «Улитка» продается предприятием по цене (30 – 2X) тыс. долл. за штуку, где Х —количество проданных мотоциклов. Переменные производственные затраты составляют 6 тыс. долл. за штуку, фиксированные затраты — 30 тыс. долл. Максимизируйте прибыль предприятия за неделю.
Предположим, что в результате изменения ставки налога с продаж последний (налог) составил дополнительно 4 тыс. долл. на каждый проданный мотоцикл.
Как изменится оптимальный выпуск мотоциклов по сравнению с начальной ситуацией?
(Решить, используя функцию Лагранжа.)
Варианты ответов:
1) увеличится на 2; 2) уменьшится на 2;
3) не изменится; 4) увеличится на 1;
5) уменьшится на 1.
Вопрос 7. Предположим, что у вас есть 2 недели (14 дней) отпуска, которые вы можете провести на Канарских островах и в Ницце. Пусть ваша функция полезности имеет вид 2KN – 3К2 – 4N2, Где К И N — количество дней, которое вы проводите на Канарских островах и в Ницце соответственно.
Сколько дней вы должны провести в Ницце, чтобы максимизировать свою функцию полезности?
(Для решения использовать функцию Лагранжа. Результат округлить до ближайшего целого. Проверить, выполняются ли условия оптимальности Куна — Таккера.)
Варианты ответов:
1) 3; 2) 4; 3) 5; 4) 6; 5) 7.
Вопрос 8. Для задачи вопроса 7 найдите значение двойственной оценки ограничения.
(Результат округлить до ближайшего целого.)
Варианты ответов:
1) 41; 2) 34; 3) 29; 4) 39; 5) 44.
Вопрос 9. Монополист планирует программу производства и реализации продукции на следующий период. Цены: Р1 = 14 – 0,25X1 (на продукт 1); Р2 = 14 – 0,5Х2 (на продукт 2), где X1 и Х2 — объемы реализации продуктов. Предположим, что вся произведенная продукция реализуется. Максимальный суммарный объем сбыта — 57.
Каков оптимальный выпуск продукта 2?
Варианты ответов:
1) 36,4; 2) 30,7; 3) 26,3; 4) 20,6; 5) 41,8.
Вопрос 10. Владелец небольшого предприятия располагает на ближайший месяц 100 тыс. руб., которые он может потратить на увеличение основных фондов К (закупку оборудования) по цене 1 тыс. руб за единицу либо на покупку дополнительной рабочей силы L по цене 50 руб./ч. Увеличение готовой продукции, которая может быть продана по 10 тыс. руб. за единицу, определяется производственной функцией F(K, L)= L2/7 К2/5.
Сколько средств следует потратить на увеличение основных фондов?
Варианты ответов:
1) 74,36 тыс. руб.; 2) 58,33 тыс. руб.; 3) 63,44 тыс. руб.;
4) 45,66 тыс. руб.; 5) 39,77 тыс. руб.
| < Предыдущая | Следующая > |
|---|