12.1. Примеры

Пример 1. Сколько производить?

Предприятие располагает ресурсами двух видов сырья и рабо­чей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продук­та, прибыль, получаемая предприятием от реализации тонны про­дукта, а также запасы ресурсов указаны в следующей таблице:

Стоимость одной тонны каждого вида сырья определяется сле­дующими зависимостями: (9 + 0,0088R1) тыс. руб. для сырья 1 и (5 - 0,0086R2) тыс. руб. для сырья 2, где R1 и R2 — затраты сырья на производство продукции. Стоимость одного часа трудозатрат определяется зависимостью (1 - 0,0002R, где R — затраты времени на производство продукции.

Вопросы:

1. Сколько продукта 1 следует производить для того, чтобы обес­печить максимальную прибыль?

2. Сколько продукта 2 следует производить для того, чтобы обес­печить максимальную прибыль?

3. Какова максимальная прибыль?

Решение. Пусть X1 — объем выпуска продукта 1 (в тоннах), Х2 — объем выпуска продукта 2 (в тоннах). Тогда задача может быть описана в виде следующей модели нелинейного программиро­вания:

При использовании программы GINO исходную информацию для решения этой задачи представляем в следующем виде:

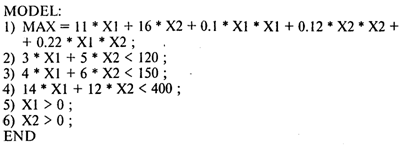
Получаем следующий результат:

Ответы: 1. 16,67т. 2.13,89т. 3. 507,407 тыс. руб.

Пример 2. Формирование портфеля ценных бумаг.

Клиент поручил брокерской конторе купить для него на 1 млн руб. акции трех известных ему компаний. Сделка заключается на год. Клиент заинтересован, с одной стороны, в максимизации сред­ней прибыли на вложенный капитал, а с другой — в минимиза­ции риска, поскольку прибыль, получаемая в конце года от ак­ции каждой компании, является величиной случайной. Известно, что чем прибыльнее акция, тем выше связанный с ней риск, по­этому названные критерии являются противоречивыми. Клиенту это обстоятельство разъяснили и попросили его указать относи­тельную значимость («вес») критериев. Клиент, будучи человеком осторожным, высказал пожелание, чтобы риск учитывался с ве­сом втрое большим, чем прибыль. Получив такие указания, со­трудники брокерской конторы сформулировали следующую мо­дель нелинейного программирования:

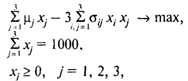
Где ХJ — объем средств, затраченных на покупку акций типа J (тыс. руб.);

MJ — математическое ожидание процента прибыли от вложения 1 тыс. руб. в акции типа J;

SJj — дисперсия указанного выше процента прибыли;

SIj — ковариация между процентами прибыли от вложения 1 тыс. руб. в акции типа I и J (I ¹ J).

Первая сумма в критерии — ожидаемое значение прибыли, обеспечиваемой пакетом акций, вторая — дисперсия прибыли пакета акций, взятая с «весом» 3. Дисперсия прибыли пакета ак­ций служит мерой риска.

Пусть средние значения процентов годовой прибыли от ак­ций компаний составляют соответственно 8, 10 и 13%. Дисперсии s11 = 0,1, s22 = 0,15, s33 = 0.19. Ковариации s12 = 0,01, s13 = 0,02, s23 = 0,03.

Вопросы:

1. Является ли целевая функция строго вогнутой?

2. Какую сумму следует вложить в покупку акций типа 1?

3. Какую сумму следует вложить в покупку акций типа 3?

Решение. Модель нелинейного (в данном случае — квадратич­ного) программирования имеет вид

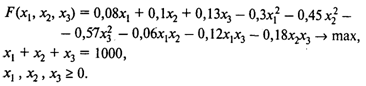
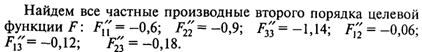
Рассчитав значения соответствующих определителей (главных миноров матрицы Хессе), можно убедиться, что выполняются условия (4), откуда следует, что целевая функция строго выпукла для любых значений х1, Х2, Х3 (значения определителей не зави­сят от значений переменных).

Используя программу GINO, исходную информацию для ре­шения этой задачи представляем в следующем виде:

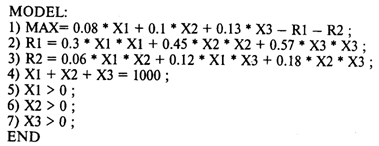
Получаем следующий результат:

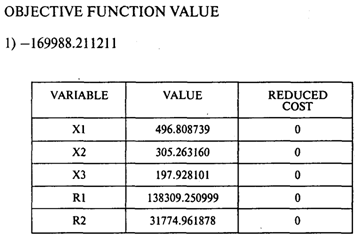
Непосредственной подстановкой полученного решения в усло­вия (5)—(8) можно убедиться, что условия Куна — Таккера выпол­няются, причем решение обеспечивает глобальный максимум це­левой функции, поскольку F строго вогнута.

Ответы: 1. Да, является (при любых значениях переменных).

2. 496,8 тыс. руб. 3. 197,93 тыс. руб.

Пример 3. Производство молочных продуктов.

Молокозавод производит для местного рынка три вида продук­тов: сметану, творог и сыр. Молоко поступает ежедневно из двух ферм. Технологические и экономические данные о производимых продуктах приведены в следующей таблице:

Затраты, связанные с приобретением сырья (молока), являют­ся кусочно-линейной функцией закупаемого количества:

А) для фермы 1

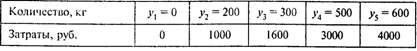
Б) для фермы 2

Вопросы:

1. Какова максимальная ежедневная прибыль молокозавода?

2. Сколько молока следует закупать на ферме 1?

3. Сколько молока следует закупать на ферме 2?

4. Как изменится максимальная прибыль, если максимальное суточное производство сметаны увеличить на 1 кг?

5. Как изменится максимальная прибыль, если максимальное суточное производство творога уменьшить на 2 кг?

Решение. Задача может быть описана с помощью модели ли­нейного программирования.

Пусть X1 — количество молока, закупаемого на ферме 1, Х2 — Количество молока, закупаемого па ферме 2. Представим Х1 и Х2 в следующем виде:

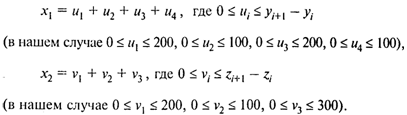
Тогда стоимость молока, закупаемого на ферме 1, описывает­ся функцией

А стоимость молока, закупаемого на ферме 2, — функцией

Окончательно модель линейного программирования имеет вид

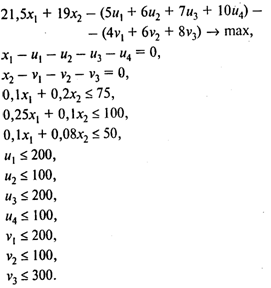
Структура матрицы задачи линейного программирования по­казана в следующей таблице:

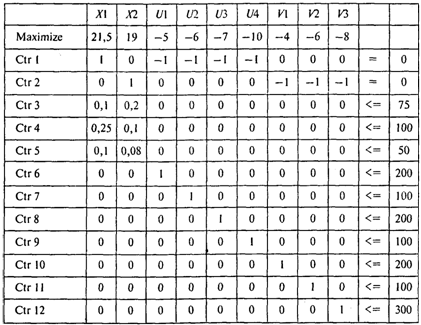
Используя для решения этой задачи программу POMWIN, по­лучаем следующий результат:

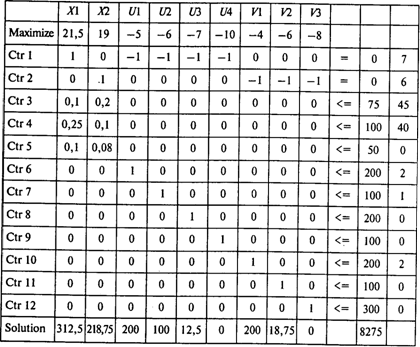
Далее представлена таблица, содержащая границы устойчиво­сти по коэффициентам целевой функции:

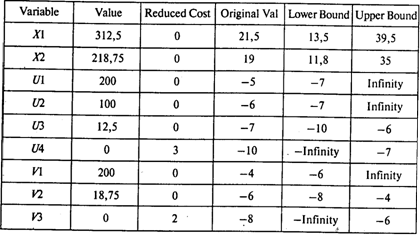
Границы устойчивости по правым частям ограничений:

Ответы: 1. 8275 руб. 2. 312,5 кг. 3. 218,75 кг. 4. Увеличится на 45 руб. 5. Уменьшится на 80 руб.

< Предыдущая		Следующая >