11.3. Задачи

Задача 1. По требованию рабочих некоторой компании проф­союз ведет с ее руководством переговоры об организации горячих обедов за счет компании. Профсоюз, представляющий интересы рабочих, добивается того, чтобы обед был как можно более качест­венным и, следовательно, более дорогим. Руководство компании имеет противоположные интересы. В конце концов стороны до­говорились о следующем. Профсоюз выбирает одну из шести фирм (Ф1 ¸ Ф6), поставляющих горячее питание, а руководство компании — набор блюд из семи возможных вариантов (B1 ¸ B7). После подпи­сания соглашения профсоюз формирует следующую платежную матрицу, элементы которой представляют стоимость набора блюд:

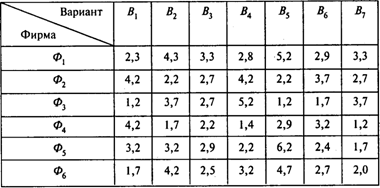
Определите оптимальные стратегии игроков и цену игры.

Вопросы:

1. Чему равна цена игры?

2. Какая фирма наиболее предпочтительна для профсоюза?

3. Какой набор руководство компании считает наиболее «вы­годным»?

4. Чему равна нижняя цена игры?

Задача 2. Известный актер обдумывает, где бы ему провести в текущем году отпуск. Он рассматривает шесть возможных вари­антов: Монте-Карло (МК), Гавайские острова (Г), Багамские ос­трова (Б), Канарские острова (К), Сочи (С), озеро Байкал (ОБ). Единственный критерий для выбора места отдыха — это стрем­ление избежать встречи с журналистами, которые могут испортить ему отпуск. Если они «выследят» актера, отдых будет испорчен (полезность равна 0). В противном случае все будет, как заплани­ровано (полезность равна 1). Журналисты могут обнаружить ак­тера с такой вероятностью: в Монте-Карло — 0,34; на Гавайских островах — 0,12; на Багамских островах — 0,16; на Канарских ост­ровах — 0,4; в Сочи — 0,5; на озере Байкал — 0,2.

Опишите данную ситуацию как игру двух лиц с нулевой сум­мой (актер — игрок 1). Вычислите цену игры и определите мини­максные стратегии обоих игроков.

Вопросы:

1. Чему равна максимальная ожидаемая полезность отпуска актера?

2. С какой вероятностью актер поедет в отпуск на Байкал?

3. Чему равна верхняя цена игры?

4. В каком из мест наиболее вероятно будет отдыхать актер?

Задача 3. На «Диком Западе» имела место следующая ситуация. Группа из пяти индейцев взяла в осаду лагерь, охраняемый че­тырьмя белыми. У лагеря два входа: E1 и Е2. Разведчик белых установил, что перед входом Е1 находится как минимум один ин­деец, а перед входом Е2 — как минимум два индейца. Остальное распределение неизвестно. Командир осажденных может себя и остальных трех человек распределить по E1 и Е2, причем у каж­дого входа должен быть как минимум один человек. Предполага­ется, что численно превосходящая (у каждого входа) группа бе­рет в плен всю группу противника без собственных потерь, в то время как при равенстве сил перед каким-либо входом потерь нет с обеих сторон. В качестве платежа (выигрыша) выступает раз­ность числа пленных.

Определите все чистые стратегии обоих противников. Построй­те платежную матрицу, считая игроком 1 обороняющуюся сторо­ну. Редуцируйте матрицу, насколько это возможно, и найдите оп­тимальные стратегии сторон.

Вопросы:

1. С какой частотой белым следует использовать стратегию: рас­положить по два человека у каждого входа?

2. Кто больше в среднем захватит пленных — белые или индейцы?

3. Какова абсолютная величина разности числа захваченных обеими сторонами пленных?

4. С какой частотой белым следует использовать стратегию:

Расположить у первого входа одного, а у второго — трех че­ловек?

5. С какой частотой индейцам следует использовать стратегию:

Расположить у первого входа трех, а у второго — двух воинов?

Задача 4. Имеются два предприятия, которые в дополнение к основной продукции могут выпускать побочную продукцию од­ного и того же назначения — пластмассовые игрушки. Известно, что они могут продавать ее в одном и том же городе. Игрушки немного отличаются по конструкции, оформлению, удобству и т. д. Первое предприятие может выпускать игрушки типа А1, А2,..., АM; Второе — типа B1, В2,..., Bn. Себестоимость и цена игрушек у всех предприятий одинаковы. Всего в течение года продается N игру­шек. Если первое предприятие выпускает игрушки типа АI, а вто­рое — типа ВJ, то первое предприятие продаст RijN игрушек, а второе — (N – RijN). Каждое предприятие стремится получить максимальный доход от продажи игрушек.

Пусть Т = 4, П = 5, N= 300 000, цена (равновесная) одной иг­рушки составляет 20 руб., элементы матрицы {Rij}4,5 представле­ны в таблице:

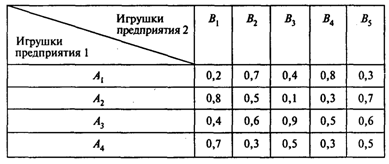
Сформулируйте игру двух лиц, считая игроком 1 первое пред­приятие. Определите выигрыш (доход от продажи) каждого пред­приятия.

Вопросы:

1. Каков общий средний доход первого предприятия?

2. Каков общий средний доход второго предприятия?

3. Какое изделие следует выпускать первому предприятию с наибольшей вероятностью?

4. Какое изделие следует выпускать второму предприятию с наибольшей вероятностью?

5. Какова частота применения стратегии «Выпускать изделие B2»?

Задача 5. Сторона В посылает подводную лодку в один из П Регионов. Сторона А, располагая Т противолодочными корабля­ми, стремится обнаружить лодку противника. Сторона B стремит­ся этого избежать. Вероятность обнаружения подводной лодки в J-м регионе одним противолодочным кораблем равна РJ (J = 1,..., N).

Предполагается, что обнаружение лодки каждым кораблем яв­ляется независимым событием. Сторона А может посылать в различные регионы разное количество кораблей (распределение Т кораблей по регионам и есть ее стратегия).

Пусть Т = 3, П = 2, Р1 = 0,4, Р2 = 0,6.

Считая сторону А игроком 1, построите игру и найдите опти­мальное распределение противолодочных кораблей по регионам.

Вопросы:

1. Каков средний выигрыш стороны А?

2. С какой частотой стороне А следует посылать в регион 2 три противолодочных корабля?

3. С какой частотой стороне А следует посылать в регион 1 один противолодочный корабль?

4. С какой частотой стороне В следует посылать подводную лодку в регион 2?

< Предыдущая		Следующая >