11.2. Вопросы
Вопрос 1. Нижняя цена матричной игры {Aij}M,N определяется следующей формулой:
![]()

Вопрос 2. Верхняя цена матричной игры {Aij}M,N определяется следующей формулой:

Вопрос 3. Какова верхняя цена следующей игры?
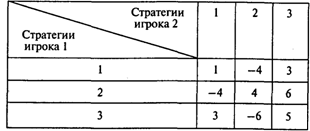
Варианты ответов:
1) 1; 2) 3; 3) 4; 4) 5; 5) 6.
Вопрос 4. Какова нижняя и верхняя цена игры для нижеприведенной матрицы?
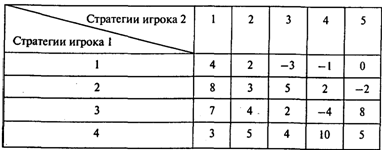
Варианты ответов:
1) (-4, 10); 2) (0, 5); 3) (2, 4); 4) (3, 5); 5) (2, 8).
Вопрос 5. Чему равно значение элемента матрицы игры в седловой точке?

Варианты ответов:
1) 6; 2) 8; 3) 15; 4) 25; 5) седловая точка отсутствует.
Вопрос 6. Используя свойство доминирования стратегий игроков, максимально редуцируйте следующую матрицу игры:

Какова размерность результирующей матрицы?
Варианты ответов:
1)1х2; 2)2х1; 3)2х2; 4)3х2; 5)3х3.
Вопрос 7. Найдите цену следующей игры (без использования пакета POMWIN):

Варианты ответов:
1) 1; 2) 1,5; 3) 2; 4) 2,5; 5) 3.
Вопрос 8. Два игрока одновременно и независимо показывают О, 1, 2 или 3 пальца. Игрок, показавший большее число пальцев, платит другому игроку сумму, равную разности чисел пальцев, показанных им и его соперником. Какова цена такой игры?
Варианты ответов:
1) 3; 2) 2; 3) 1; 4) 0; 5) –1.
Вопрос 9. Два игрока одновременно и независимо показывают 1, 2 или 3 пальца. Пусть S — сумма чисел пальцев, показанных обоими противниками. Если S — нечетное, то игрок 1 платит другому игроку сумму S, если же S — четное, эту сумму выплачивает игрок 2. Чему равна цена такой игры?
Варианты ответов:
1) –1; 2) 0; 3) 1; 4) 1,3; 5) 1,7.
Вопрос 10. Постройте платежную матрицу следующей игры.
Игрок 2 прячет в одном из П мест предмет стоимостью СJ (J = 1,.... N). Игрок 1 ищет этот предмет в одном из П мест, и если находит, то получает СJ, в противном случае получает 0. Пусть П = 4 и вектор стоимости предметов с = (5, 7, 3, 12). Чему равна цена игры?
Варианты ответов:
1) 1,75; 2) 1,57; 3) 1,32; 4) 1,23; 5) 1,12.
| < Предыдущая | Следующая > |
|---|