11.1. Примеры

Пример 1. Выбор стратегии. Матрица некоторой игры имеет вид

Найдите оптимальные стратегии игроков.

Решение. В этой игре игрок 1 имеет три возможные страте­гии: А1, а2, А3 из, а игрок 2 — четыре возможные стратегии: B1, B2, B3, B4.

Рассмотрим процесс принятия игроками решения (предпола­гается, что они действуют рационально). Взглянув на таблицу, можно заметить, что если игрок 1 не знает, как поступит его про­тивник, то, действуя наиболее целесообразно и считая, что про­тивник будет действовать подобным же образом, он выберет стра­тегию А2, которая гарантирует ему наибольший из трех возмож­ных наименьших выигрышей: 9, 13, 8. Другими словами, игрок 1 руководствуется принципом максиминного выигрыша. Этот выигрыш a = АIj есть нижняя цена игры. Для нашего примера a = 13.

Игрок 2 рассуждает аналогично: если он выберет стратегию B1, ,то потеряет самое большее 23, если стратегию B2, то — 40, и т. д. В результате он выберет стратегию B3, которая гарантирует ему наименьший из четырех возможных проигрышей: 23, 40, 13, 25. Принято говорить, что игрок 2 руководствуется принципом мини­максного проигрыша. Этот проигрыш b = АIj есть верхняя цена игры. Для нашей матрицы b = 13.

Ситуация (A2, B3) есть седловая точка, и a = b = 13 есть цена игры.

При наличии седловой точки ни одному из участников игры невыгодно отклоняться от своей минимаксной стратегии: он бу­дет наказан противником тем, что получит меньший выигрыш.

Пример 2. Где строить?

Две конкурирующие крупные торговые фирмы Ф1 и Ф2 пла­нируют построить в одном из четырех небольших городов Г1, Г2, Г3 и Г4, лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и чис­ленность населения показаны на рис. 1.

Рис. 1

Прибыль каждой фирмы зависит от численности населения городов и степени удаленности универсамов от места жительства потенциальных покупателей. Специально проведенное исследова­ние показало, что прибыль в универсамах будет распределяться между фирмами следующим образом:

Например, если универсам фирмы Ф1 расположен к городу Г1 ближе универсама фирмы Ф 2, то прибыль от покупок, сделанных жителями данного города, распределится следующим образом: 75% получит Ф1, остальное — Ф 2.

Представьте описанную ситуацию как игру двух лиц.

В каких городах фирмам целесообразно построить свои уни­версамы?

Решение. Составим платежную матрицу игры, в которой иг­роком 1 будет фирма Ф 1, а игроком 2 — фирма Ф2. Стратегии обо­их игроков: строить свой универсам в городе Г1, в городе Г2 и т. д. Элементы матрицы — прибыль фирмы Ф1 (в тыс. руб.), которая, как предполагается, пропорциональна (причем с одним и тем же коэффициентом) числу покупателей. Величина указанного коэф­фициента пропорциональности для выбора оптимального места размещения универсамов значения не имеет, поэтому примем его равным единице.

Платежная матрица имеет вид

Рассмотрим примеры расчета значений элементов (Г1, Г2) и (Г3, Г4) матрицы.

Ситуация (Г1, Г2) означает, что фирма Ф1, строит универсам в городе Г1, а фирма Ф2 — в городе Г2. Число покупателей фирмы Ф1 складывается из покупателей четырех городов. Для ситуации (Г1, Г2) число покупателей из Г1: 0,75×30, из Г2: 0,45×50, из Г3 0,45×40, из Г4: 0,45×30, т. е. в сумме 76,5 тыс. руб. Для ситуации (Г3, Г4) число покупателей из Г1: 0,75×30, из Г2: 0,75×50, из Г3: 0,75×40, из Г4: 0,45×30, т. е. в сумме 103,5 тыс. руб. Элементы мат­рицы выигрышей фирмы Ф2 — дополнения до числа 150 (общее число жителей в четырех городах). Таким образом, имеет место игра двух лиц с ненулевой постоянной суммой, оптимальные стратегии которой те же, что и для соответствующей игры с ну­левой суммой.

Полученная платежная матрица имеет седловую точку (Г2, Г2). Соответствующий элемент матрицы равен 90.

Таким образом, обеим фирмам следует строить свои универ­самы в одном и том же городе Г2, при этом прибыль фирмы Ф1 составит 90 тыс., а фирмы Ф2 — 60 тыс. руб.

Пример 3. Двухпальцевая «игра морра».

Каждый игрок показывает один или два пальца и называет число пальцев, которое, по его мнению, показал его противник (ни один из игроков не видит, какое число пальцев на самом деле показывает его противник). Если один из игроков угадывает правильно, он выигрывает сумму, равную сумме числа пальцев, по­казанных им и его противником. В противном случае (если ни­кто не угадывает) — ничья. Если оба угадали, то игроки платят друг другу одинаковую сумму, в результате также ничья.

Вопросы:

1. Существует ли в данной игре седловая точка в чистых стра­тегиях?

2. Кто из игроков в среднем выигрывает и сколько?

3. Как часто игрок 1 должен говорить, что его противник по­казал два пальца?

4. Как часто игрок 2 должен показывать один палец?

Решение. Прежде всего определим стратегии игроков и по­строим платежную матрицу.

Стратегиями игрока 1 (строки таблицы) являются четыре пары чисел. Первое число каждой пары — это число пальцев, показан­ное им, второе — число пальцев, которое, как он предполагает, показал его противник. Такие же стратегии имеет игрок 2.

Платежная матрица размером 4 х 4 и другая информация пред­ставлены в следующей таблице:

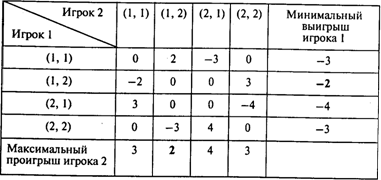
Нижняя цена игры a = –2, верхняя цена игры b = 2.

Как видим, a ¹ b, поэтому седловой точки не существует и ре­шение в чистых стратегиях отсутствует. Для решения данной игры построим соответствующую задачу линейного программирования. Для этого сначала преобразуем платежную матрицу таким обра­зом, чтобы все ее элементы были положительными. Максималь­ное по абсолютной величине значение неположительного элемента платежной матрицы равно 4, поэтому к матрице достаточно при­бавить число 5:

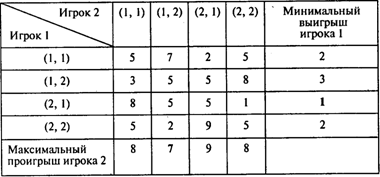
Оптимальная стратегия игрока 1 находится решением следу­ющей задачи линейного программирования [см. (1)]:

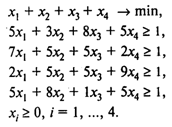
Используя пакет POMWIN, исходную информацию для реше­ния этой задачи можно представить в виде следующей таблицы:

Получаем следующий результат:

Решение (в нижней строке):

Оптимальное значение целевой функции равно 0,2.

В последнем столбце — двойственные оценки. Переходя к переменным исходной задачи и учитывая, что v = 1/(X1 + Х2 + х3 + Х4) = 5 и Pi = ХI v, получаем:

P1 = 0, р2 = 0,5715, P3 = 0, p4 = 0,4285.

Это означает, что при многократном повторении игры первая стратегия (1, 1) и третья стратегия (2,1) игроком 1 не должны ис­пользоваться; вторая стратегия (1,2) должна использоваться с ча­стотой 0,5715, четвертая стратегия (2, 2) — с частотой 0,4285.

Аналогично определяем оптимальную стратегию игрока 2:

Т. е. игрок 2 должен использовать лишь свою вторую стратегию (1,2) с частотой 0,5715 и третью стратегию (2, 1) с частотой 0,4285.

Так как исходная матрица была увеличена на 5, получаем, что цена первоначальной игры равна 0 (5 — 5). Таким образом, исход игры — ничья.

Ответы: 1. Нет, не существует. 2. Ничья. 3. Всегда. 4. 0,572.

Пример 4. Доминирование стратегий.

Платежная матрица для двух игроков имеет вид

Преобразуйте игру, исключив доминируемые стратегии.

Решение. Для игрока 1: вторая стратегия (строка 2 матрицы) доминирует четвертую и шестую стратегии, поэтому четвертую и шестую строки можно вычеркнуть. Для игрока 2: третья страте­гия (столбец 3) доминирует четвертую, поэтому четвертый стол­бец можно вычеркнуть, и т. д.

Результирующая матрица имеет вид

Пример 5. Как завоевать рынок?

Два конкурирующих друг с другом предприятия, выпускающие стиральные машины, имеют следующие доли общего сбыта своей продукции на местном рынке: 53% — предприятие 1 и 47% — предприятие 2.

Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: A1 (B1) — расширить сеть сбыта; A2 (B2) — рекламировать свою продукцию; A3(B3) — увеличить ассортимент (число моделей стиральных машин); A4 (B4) — ничего не предпринимать.

Анализ показал, что при осуществлении обоими предприяти­ями указанных мероприятий доля (в %) предприятия 1 на рынке стиральных машин изменится следующим образом:

Сформулируйте данную ситуацию в виде игры.

Вопросы:

1. Какое из мероприятий предприятия 1 наиболее эффективно?

2. Какую долю на рынке будет иметь предприятие 1?

3. Какое из мероприятий предприятия 2 наиболее эффективно?

4. С какой частотой следует предприятию 2 использовать стра­тегию «реклама»?

Решение. Приведенную выше таблицу можно рассматривать как платежную матрицу игры двух лиц с нулевой суммой. Альтер­нативы, имеющиеся в распоряжении предприятий, — стратегии игроков. Прежде всего следует исключить доминируемые страте­гии игроков: 04 игрока 1 и 64 игрока 2. В результате получим

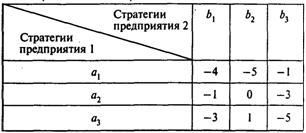
Увеличив все элементы матрицы на 6, решим следующую за­дачу линейного программирования:

Используя пакет POMWIN, получаем следующий результат:

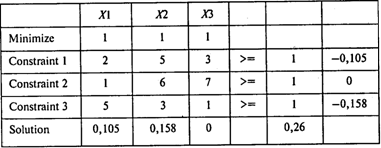
Переходя к переменным исходной задачи и учитывая, что v = 1/(X1 + X2 + Х3) = 3,85 и Pi = XiV, получаем: Р1 = 0,4, Р2 = 0,6, P3 = 0, P4 = 0. Цена игры, соответствующая первоначальной мат­рице, равна –2,15 (3,85 – 6). Таким образом, предприятие 1 при многократном повторении игры должно использовать с частотой 0,4 стратегию А1 (расширить сеть сбыта), с частотой 0,6 — страте­гию A2 (рекламировать свою продукцию), а стратегии A3 (увели­чить ассортимент) и A4 (ничего не предпринимать) не использо­вать вовсе. При этом доля сбыта предприятия на рынке уменьшит­ся на 2,15%. Оптимальная смешанная стратегия предприятия 2: с частотой 0,4 использовать стратегию B1 (расширить сеть сбыта) и с частотой 0,6 — стратегию B3 (увеличить ассортимент). Страте­гии A2 (рекламировать свою продукцию) и A4 (ничего не делать) не применять вовсе. Доля предприятия 2 на рынке увеличится на 2,15%. Казалось бы, поскольку в результате осуществления своих мероприятий предприятие 1 «теряет рынок», ему не следует ни­чего предпринимать, однако в этом случае оно потеряет еще боль­ше (в соответствии со стратегией A4) из-за действий предприятия 2, которому они выгодны.

Ответы: 1. Реклама. 2. 50,85%. 3. Увеличение ассортимента. 4. С нулевой частотой, т. е. стратегия «реклама» пред­приятием 2 вообще не должна применяться.

< Предыдущая		Следующая >