11. Стратегические игры

Цели

В данной главе показаны возможности использования одного из классов игровых моделей — так называемых стратегических игр — для принятия решений преимущественно экономического ха­рактера в условиях неопределенности. Дается общее описание страте­гической игры и ее место в классификации игр. Подробно рас­сматривается класс стратегических игр двух лиц с нулевой, а также с постоянной ненулевой суммой. Определяется понятие равнове­сия в ифе в чистых и смешанных стратегиях. Представлен общий подход к играм указанного типа — сведение к соответствующей задаче линейного программирования.

После того как вы выполните предлагаемые в этой главе зада­ния, вы будете уметь строить для различных ситуаций принятия экономических решений (там, где это возможно и целесообраз­но) соответствующую игровую модель, определяя:

• игроков и их стратегии;

• матрицу выигрышей;

• наличие или отсутствие седловых точек в чистых стратегиях;

• доминируемые стратегии;

• эквивалентную модель линейного программирования;

• оптимальные стратегии;

• цену игры.

Модели

Методы, основанные на теории игр, используются для приня­тия решений в условиях неопределенности. Игра — это матема­тическая модель конфликтной ситуации, которая предполагает на­личие следующих компонентов:

А) заинтересованных сторон;

Б) возможных действий каждой из сторон;

В) интересов сторон.

В игре заинтересованные стороны называются Игроками, каж­дый из которых может предпринимать не менее двух действий (если ифок имеет в своем распоряжении только одно действие, то он фактически не участвует в игре, поскольку заранее извест­но, что он предпримет).

Слово «игра» обозначает некоторый набор правил и соглаше­ний, составляющих данный вид игры, например: футбол, шахма­ты и др.

В экономике модель поведения лиц в виде игры возникает, например, при попытке нескольких фирм завоевать наиболее вы­годное место на конкурентном рынке или при желании несколь­ких лиц (компаний) разделить некоторое количество продукта (ресурса, финансовых средств) между собой так, чтобы каждому досталось как можно больше. Игроками в конфликтных эконо­мических ситуациях, моделируемых в виде игры, являются про­изводственные и непроизводственные фирмы, банки, отдельные предприниматели и другие экономические агенты. В военной области модель игры используется, например, для наилучшего выбора средств (из имеющихся или потенциально возможных) поражения военных целей противника или защиты от его напа­дения.

Для игр характерна Неопределенность результата (исхода). При­чины неопределенности относятся к трем группам:

1) комбинаторные источники (шахматы);

2) влияние случайных факторов (игра в орлянку, кости, кар­точные игры, где случаен расклад);

3) стратегическое происхождение: игрок не знает, какого об­раза действий придерживается его противник. Здесь неопределен­ность исходит от другого лица.

Игры, в которых неопределенность имеет стратегическое проис­хождение, называются Стратегическими.

Таким образом, в стратегической игре действия предпринима­ют две стороны или более, в отличие от нестратегической игры, в которой действия предпринимает одна сторона, а остальные яв­ляются заинтересованными сторонами.

Стратегические игры классифицируют по следующим при­знакам:

1) число игроков (игра двух лиц, игра П (п > 2) лиц);

2) количество стратегий (конечные, бесконечные);

3) количество информации, имеющейся у игроков относитель­но прошлых ходов (игры с полной, игры с неполной информаци­ей). Шахматы — пример игры с полной информацией;

4) принцип деления выигрыша (коалиционные, бескоалици­онные).

Далее рассматривается модель конечной стратегической игры с полной информацией, в которой участвуют две стороны, име­ющие противоположные интересы. Такую игру принято называть Конечной игрой двух лиц с нулевой суммой.

1. Матричная игра двух лиц с нулевой суммой

В Игре двух лиц с нулевой суммой (такую игру называют также Антагонистической) принимают участие два игрока: игрок 1 и иг­рок 2. В распоряжении каждого из них имеется множество стра­тегий. Под Стратегией понимают совокупность правил (принци­пов), определяющих выбор варианта действий при каждом ходе игро­ка в зависимости от сложившейся ситуации. Пусть А = {А1, а2,...} — Множество стратегий игрока 1, В = {B1, B2,...} — множество стра­тегий игрока 2. Элементы множества А — возможные стратегии (действия) игрока 1, элементы множества В — стратегии игрока 2. Условия игры представлены так называемой Функцией выигрыша Игрока 1: H(Ai, Bj), где АIÎА — i-я стратегия игрока 1, BjÎВ — j-я стратегия игрока 2. В игре с нулевой суммой выигрыш игрока 2 равносилен проигрышу игрока 1 и равен поэтому — H(Ai, Bj). Пред­полагается, что функция выигрыша обоим игрокам известна. По­скольку игроков всего двое и игра антагонистическая, коалиции невозможны.

Игра, в которой множества А и В стратегий игроков конечны, т. е. |А| < ¥, |В| < ¥, называется Матричной. В этом случае функ­ция выигрышей игрока 1 имеет вид матрицы, называемой Матри­цей игры (матрицей выигрышей, платежной матрицей) Н = {АIj}M,N, I = 1,..., Т; J = 1,..., П. Строки этой матрицы соответствуют стра­тегиям A1, А2, ..., АM игрока 1, столбцы — стратегиям B1, B2, ..., Bn игрока 2. Элемент матрицы Aij = H (Ai, Bj) — выигрыш игрока 1 в случае, когда он применит стратегию АI, а его противник — стра­тегию Bj, I = 1, ..., Т; J = 1, ..., П.

Элементы матрицы могут быть положительными, отрицатель­ными или равными нулю. Случай, когда данный элемент матри­цы Положителен, означает, что игрок 2 в определенной ситуа­ции должен уплатить игроку 1 сумму, равную значению этого эле­мента. Если данный элемент Отрицателен, игрок 1 уплачивает игроку 2 сумму, равную абсолютному значению этого элемента. И наконец, если этот элемент равен Нулю, никакой выплаты не производится. Таким образом, в игре двух лиц с нулевой суммой один игрок выигрывает столько же, сколько проигрывает другой (все выплаты производятся из «карманов» противников). Это и объясняет название — игра с нулевой суммой.

Игрок 1 стремится к максимальному выигрышу, игрок 2 — к минимальному проигрышу. Решить игру — значит найти опти­мальные стратегии игроков и их выигрыши.

В игре двух лиц с нулевой суммой, как и в любой другой стра­тегической игре, исход зависит от поведения обоих игроков, ко­торое основывается на так называемых правилах игры. Допустим, что по правилам игры игрок 1 может выбрать произвольную стро­ку матрицы и, следовательно, может выбрать одно из чисел 1, 2, ..., Т. Аналогично игрок 2 имеет возможность выбора произ­вольного столбца матрицы выигрышей и, следовательно, одного из чисел 1, 2,..., П. Исход (результат) игры и, следовательно, сум­му, которую игрок 2 должен уплатить игроку 1, определяет эле­мент матрицы выигрышей, находящийся на пересечении строки, выбранной игроком 1, и столбца, выбранного игроком 2. Ни один из партнеров не знает, какую стратегию применит его противник. Таким образом, имеет место ситуация полной неопределенности, при которой теория вероятностей не может помочь игрокам в выборе решения.

Рассмотрим процесс принятия решений обеими сторонами более детально, предполагая, что игроки действуют рационально.

Если игрок 1 не знает, как поступит его противник, то, дей­ствуя наиболее целесообразно, не желая рисковать и считая, что противник также будет действовать целесообразно, он выберет такую стратегию, которая гарантирует ему Наибольший из наи­меньших выигрышей при любой стратегии противника. Принято говорить, что при таком образе действий игрок 1 руководству­ется Принципом максиминного выигрыша. Этот выигрыш определя­ется формулой a = Aij. Величина a называется Нижней ценой игры, максиминным выигрышем, или сокращенно — Максимином.

В свою очередь игрок 2, действуя рационально, выберет такую стратегию, которая гарантирует ему Наименьший из Возможных проигрышей при любых действиях противника. Принято гово­рить, что игрок 2 руководствуется Принципом минимаксного проиг­рыша. Этот проигрыш определяется выражением b = . Величина b называется Верхней ценой игры или Минимаксом.

Принцип осторожности, который определяет выбор партнера­ми стратегий, соответствующих максиминному выигрышу или минимаксному проигрышу, часто называют Принципом минимакса, а стратегии, вытекающие из этого принципа, — Минимаксны­ми стратегиями. Доказано, что всегда а 5 р, чем и объясняются названия «нижняя цена» и «верхняя цена». В случае когда ниж­няя цена игры равняется ее верхней цене, их общее значение на­зывается Ценой игры. При этом результат стратегической игры двух лиц с нулевой суммой можно определить, не приступая к факти­ческой игре: вполне реален сценарий, когда партнеры, взглянув на матрицу, рассчитываются, пожимают друг другу руки и рас­ходятся. Очевидно, что исход такой игры не изменится, если она будет повторена многократно, поскольку ни одному из игроков невыгодно отклоняться от своих минимаксных стратегий. Си­туация, в которой нижняя и верхняя цены игры совпадают, на­зывается Седловой точкой. Формальное определение: ситуация (Ai*, Bj*) ÎA ´ В называется седловой точкой, если

В седловой точке элемент матрицы АIj* = H(Ai*, Bj*) является од­новременно наименьшим в строке и наибольшим в столбце и, сле­довательно, соответствует цене игры. Однако существуют матри­цы игры двух лиц с нулевой суммой (и таких игр большинство), для которых a ¹ b, т. е. седловая точка отсутствует. Исход такой игры определить труднее, поскольку какой-либо одной так назы­ваемой Чистой оптимальной стратегии ни для одного игрока не существует. В таких случаях говорят, что решение игры в чистых стратегиях отсутствует, и рассматривают так называемое Смешан­ное расширение игры, решение которой ищут в смешанных страте­гиях. Смешанная стратегия игрока — это случайная величина, зна­чениями которой являются его чистые стратегии. Для того чтобы задать смешанную стратегию игрока, необходимо указать вероят­ности (частоты), с которыми выбираются его первоначальные (чи­стые) стратегии. При этом предполагается, что игра повторяется многократно.

Здесь Р1, р2,..., рM — вероятности использования игроком 1 в смешанной стратегии своих чистых стратегий A1, A2, ..., Am; Q1, Q2, ..., Qn — вероятности использования игроком 2 в смешан­ной стратегии своих чистых стратегий B1, B2, ..., Bn.

Математическое ожидание выигрыша игрока 1:

Смешанная стратегия, которая гарантирует данному игроку наибольший возможный средний выигрыш (или наименьший воз­можный средний проигрыш), называется его Оптимальной смешанной стратегией, а стратегии, из которых складывается оптималь­ная смешанная стратегия, определяются как Выгодные стратегии.

Пусть Р* — смешанная стратегия игрока 1,Q* — смешанная стратегия игрока 2. Ситуацию (P*,Q*), при которой М(Р, Q*) £ М(Р*, Q*) £ М(Р*, Q), называют Седловой точкой смешанного расширения игры, а математическое ожидание выигрыша v = М(Р*, Q *) — Ценой игры, причем всегда a £ v £ b.

Доминирование стратегий. Если платежная матрица такова, что каждый элемент некоторой строки I Не меньше соответствующе­го элемента строки K и по меньшей мере один ее элемент Строго больше соответствующего элемента строки K, то говорят, что стра­тегия а, игрока 1 Доминирует его стратегию АI. Доминируемая стра­тегия не может быть оптимальной чистой стратегией игрока 1 и даже не может войти в его оптимальную смешанную стратегию с ненулевой вероятностью, поэтому ее можно исключить из рас­смотрения, вычеркнув из матрицы строку K. Аналогично: если каждый элемент некоторого столбца J Не больше соответству­ющего элемента столбца R и по меньшей мере один его элемент Строго меньше соответствующего элемента столбца R, то гово­рят, что стратегия Bj игрока 2 Доминирует его стратегию Br. Поэтому столбец R матрицы можно вычеркнуть.

Сведение игры двух лиц с нулевой суммой к задаче линейного программирования. Если седловая точка отсутствует, то общим методом решения игры любой (конечной) размерности является сведение игры двух лиц с нулевой суммой к задаче линейного профаммирования. Из основного положения теории стратегичес­ких игр следует, что при использовании смешанных стратегий существует по меньшей мере одно оптимальное решение с ценой игры v, причем a £ v £ b, т. е. цена игры находится между ниж­ним и верхним значениями игры. Величина v неизвестна, но мож­но предположить, что v > 0. Это условие выполняется, поскольку путем преобразования матрицы всегда можно сделать все ее эле­менты положительными. Таким образом, если в исходной платеж­ной матрице имеется хотя бы один Неположительный элемент, то первым шагом в процедуре сведения игры к задаче линейного программирования должно быть ее преобразование в матрицу, Все Элементы которой Строго положительны. Для этого достаточ­но увеличить все элементы исходной матрицы на одно и то же число D > |Aij|, где АIj £ 0. При таком преобразовании мат­рицы оптимальные стратегии игроков не изменяются.

Допустим, что смешанная стратегия игрока 1 складывается из стратегий A1, A2,..., Am с вероятностями соответственно P1, P2,..., Pm (, ). Оптимальная смешанная стратегия игрока 2 скла­дывается из стратегий B1, B2,..., Bn с вероятностями Q1, Q2,..., Qn (, ). Условия игры определяются платежной матрицей , , I = 1,..., M; J = 1,..., N.

Если игрок 1 применяет оптимальную смешанную стратегию, а игрок 2 — чистую стратегию Bj, то средний выигрыш игрока 1 (математическое ожидание выигрыша) составит Р1A1J + р2A2J + ... + РMAmj, J = 1,..., N.

Игрок 1 стремится к тому, чтобы при любой стратегии игрока 2 его выигрыш был не менее чем цена игры v и сама цена игры была максимальной. Такое поведение игрока 1 описывается следующей моделью линейного программирования:

V ® max (игрок 1 стремится максимизировать свой выигрыш),

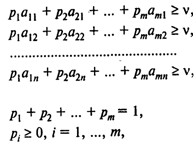
Или, обозначив ХI = РI/v, имеем

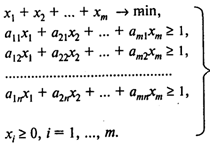
Причем

Поведению игрока 2 соответствует двойственная задача:

Задача (1) всегда имеет решение. Получив ее оптимальное решение , можно найти цену игры оптимальные значения и, следовательно, оптималь­ную стратегию игрока 1. Если исходная матрица увеличивалась на D, то для получения цены первоначальной игры v* нужно умень­шить на D.

Справедливо и обратное положение: любую задачу линейного программирования можно свести к решению соответствующей игры двух лиц с нулевой суммой.

2. Матричная игра двух лиц с ненулевой постоянной суммой

Конечная игра, в которой сумма выигрышей обоих игроков не равна нулю и постоянна для всех сочетаний их чистых стратегий, называется матричной игрой двух лиц с ненулевой постоянной сум­мой. Пусть — матрица выигрышей игрока 1 и — матрица выигрышей игрока 2. Причем для всех .

Такого рода игра сводится к игре двух лиц с нулевой суммой следующим образом:

1) каждому игроку выплачивается сумма С/2;

2) решается игра с нулевой суммой с матрицей выигрышей игрока 1, где

Действительно, в игре с преобразованной таким способом мат­рицей выигрышей игрок 2 получает сумму С/2 – АIj для всех I = 1, ..., Т; J = 1, ..., П, т. е. новая игра является игрой с нулевой суммой. При этом каждый игрок ничего не теряет от того, что каждый из них в игре получает на С/2 меньше, поскольку по С/2 они получили перед игрой.

< Предыдущая		Следующая >