11. Геометрические приложения определенного интеграла

1. Вычисление площади плоской фигуры. а) Рассмотрим фигуру, ограниченную графиком непрерывной, неотрицательной на промежутке [A;B] функции F(X), отрезком [A;B] оси OX, и прямыми X=A, X=B. Такую фигуру называют Криволинейной трапецией. Площадь S Этой трапеции определяется формулой

.

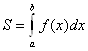Б) Если F(X)<0 во всех точках промежутка [A;B] и непрерывна на этом промежутке, то площадь криволинейной трапеции, ограниченной отрезком [A;B] горизонтальной оси координат, прямыми X=a, X=b и графиком функции Y=f(X), определяется формулой

.

в) Если криволинейная трапеция ограничена линиями , то справедлива формула

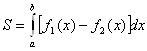
Г) Если кривая задана параметрическими уравнениями

, ,

То площадь криволинейной трапеции, ограниченной этой кривой, прямыми X=a, X=b И отрезком [A;B] горизонтальной оси координат находится по формуле

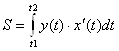
Где T1 и T2 определяются из уравнений

, .

Д) Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя полярными радиусами , , где , выражается интегралом

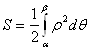
2. Вычисление длины дуги плоской кривой. а) Если кривая 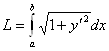на отрезке [A;B] – гладкая, то длина соответствующей дуги этой кривой находится по формуле . б) При параметрическом задании кривой

, ,

длина дуги кривой, соответствующая монотонному изменению параметра T От T1 до T2, вычисляется по формуле 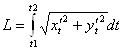. в) Если гладкая кривая задана в полярных координатах уравнением 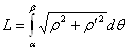, , то длина дуги равна . 3. Вычисление объема тела вращения. а) Если криволинейная трапеция, ограниченная кривой 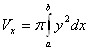и прямыми , , , вращается вокруг оси OX, то объем тела вращения вычисляется по формуле б) Если фигура, ограниченная кривыми 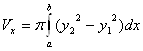, и прямыми , , вращается вокруг оси OX, то объем тела вращения вычисляется по формуле 4. Вычисление площади поверхности вращения. а) Если дуга гладкой кривой 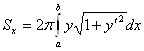() вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле . б) При параметрическом задании кривой

, ,

где .

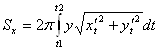Пример 1. Найти площадь фигуры ограниченной линиями

.

Решение.

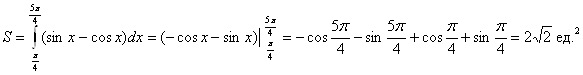
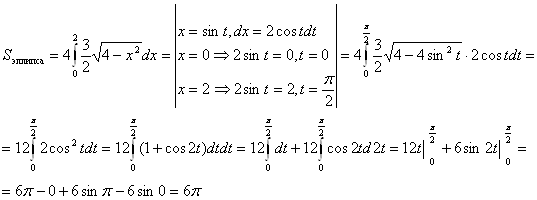
Пример 2.Найти площадь эллипса . т. е. .

Решение. Из условия

< Предыдущая		Следующая >