30. Вычисление площади поверхности

Пусть поверхность задана параметрически 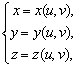или в векторной форме

.

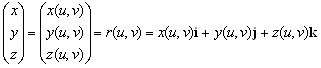Рассмотрим кусок поверхности, ограниченный линиями 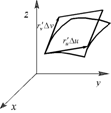. Из геометрического смысла производной следует, что вектор является касательным к кривой в точке, а вектор будет касательным вектором кривой в той же точке. Далее,

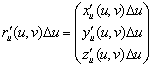Где и - бесконечно малые более высокого порядка малости, чем и . Можно показать, что площади криволинейного четырёхугольника и параллелограмма, лежащего в касательной плоскости и построенного на векторах и 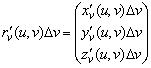, отличаются на бесконечно малую более высокого порядка малости, чем . Поэтому заменим четырёхугольник указанным параллелограммом. Площадь этого параллелограмма равна . Проводя построения, аналогичные построениям в определении двойного интеграла, получаем, что площадь поверхности равна

Пусть поверхность задана явно уравнением . Всякую такую поверхность можно задать параметрически (взяв в качестве параметров ) или в векторной форме уравнением . Тогда

, ,

.

Поэтому и площадь поверхности может быть найдена по формуле

Примеры

1. Вычислить площадь поверхности , если область задаётся неравенством .

Так как , , то, подставляя в формулу площади поверхности, имеем . Переходя к полярным координатам, получаем = .

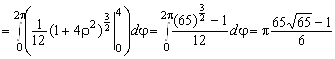2. Вычислить площадь поверхности сферы.

Параметрическое уравнение сферы радиуса можно написать в виде , где

, или, что то же самое, в векторной форме

. Тогда

,

Поэтому

.

Вычисляя модуль этого вектора, получаем . Поэтому .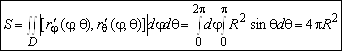

< Предыдущая		Следующая >