14. Замена переменных в определённом интеграле

Иногда возникает необходимость перейти в интеграле к новой переменной. Имеет место следующий результат.

Теорема 2.7. Пусть интегрируема на отрезке и - дифференцируемое биективное (взаимно однозначное) отображение, такое, что . Тогда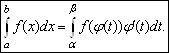

Доказательство. Докажем теорему в предположении, что функция интегрируема на отрезке .Это выполнено, например, когда функции и имеют конечное число точек разрыва первого рода (кусочно непрерывны), так как в этом случае функция также кусочно непрерывна и, по следствию из теоремы 2.3, интегрируема. Разобьём отрезок на части точками . Этому разбиению отрезка соответствуют разбиение отрезка точками . Так как дифференцируема, то, по теореме Лагранжа о конечных приращениях , , где - некоторая точка. Положим . Составим интегральную сумму

.

В левой части этого равенства стоит интегральная сумма для интеграла , а справа - для интеграла . Так как оба интеграла существуют, то, переходя в этом равенстве к пределу по всевозможным разбиениям, получаем справедливость утверждения теоремы.

Примеры.

1. Вычислить интеграл Положим Тогда , и поэтому исходный интеграл равен

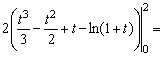
2. Вычислить интеграл Положим . Тогда , и поэтому

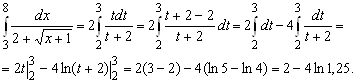
ЗАдание 2.3

Вычислить интегралы

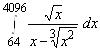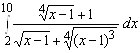1. ; 2. ; 3. ;

4. .

Ответы: 1. ; 2. ; 3. ; 4. .

< Предыдущая		Следующая >