12. Интеграл как функция верхнего предела. Формула Ньютона-Лейбница
Рассмотрим функцию ![]() . Эту функцию называют: интеграл как функция верхнего предела. Отметим несколько свойств этой функции.
. Эту функцию называют: интеграл как функция верхнего предела. Отметим несколько свойств этой функции.
Теорема 2.5. Если ![]() интегрируемая на
интегрируемая на ![]() функция, то
функция, то ![]() непрерывна на
непрерывна на ![]() .
.
Доказательство. По свойству 9 определенного интеграла (теорема о среднем) имеем ![]() , откуда, при
, откуда, при ![]() , получаем требуемое.
, получаем требуемое.
Теорема 2.6. Если ![]() непрерывная на
непрерывная на ![]() функция, то функция
функция, то функция ![]() дифференцируема на
дифференцируема на ![]() и
и ![]() .
.
Доказательство. По свойству 10 определенного интеграла (вторая теорема о среднем), имеем ![]() где С – некоторая точка отрезка
где С – некоторая точка отрезка ![]() . В силу непрерывности функции
. В силу непрерывности функции ![]() Получаем
Получаем
![]() .
.
Доказанная теорема решает задачу восстановления первообразной для непрерывной функции с помощью интеграла как функции верхнего предела и даёт конструктивное доказательство (то есть доказательство с построением объекта, существование которого утверждается) теоремы 1.1. Более того, если функция ![]() имеет на отрезке
имеет на отрезке ![]() конечное число точек разрыва первого рода, то, разбивая отрезок
конечное число точек разрыва первого рода, то, разбивая отрезок ![]() на участки непрерывности функции
на участки непрерывности функции ![]() , получаем, что с помощью интеграла как функции верхнего предела можно восстановить обобщённую первообразную и в этом случае, а заодно и установить справедливость теоремы 1.2.
, получаем, что с помощью интеграла как функции верхнего предела можно восстановить обобщённую первообразную и в этом случае, а заодно и установить справедливость теоремы 1.2.
Таким образом, ![]() - одна из первообразных функции
- одна из первообразных функции ![]() следовательно,
следовательно, ![]() Где
Где ![]() - другая первообразная
- другая первообразная ![]() Далее, так как
Далее, так как ![]() то
то ![]() следовательно,
следовательно, ![]() и поэтому
и поэтому ![]() Полагая
Полагая ![]() , получаем формулу Ньютона-Лейбница
, получаем формулу Ньютона-Лейбница
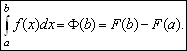
Из формулы Ньютона-Лейбница следует, что для вычисления определённых интегралов мы можем применять весь набор приёмов и методов нахождения неопределённых интегралов.
Примеры
1. 

Задание 2.1
Вычислить интегралы:
1. ; 2.
; 2.![]() ; 3.
; 3.![]() ; 4.
; 4.![]() ;
;
5.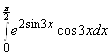 ; 6.
; 6. ![]() ; 7.
; 7.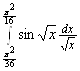 ; 8.
; 8. .
.
Ответы: 1. ![]() ; 2.
; 2. ![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() ;
;
5. ![]() ; 6.
; 6. ![]() ; 7.
; 7. ![]() ; 8.
; 8. ![]() .
.
| < Предыдущая | Следующая > |
|---|