10. Гамильтоновы графы

Определение. Гамильтоновым называется Простой цикл в графе, содержащий Все вершины графа по одному разу. Граф с таким циклом называется Гамильтоновым.

Гамильтонов цикл не обязательно содержит Все ребра данного графа. Гамильтонов граф является важной разновидностью Связного графа.

Критерий существования гамильтонова цикла в графе пока неизвестен. Сформулированы достаточные условия существования гамильтонова цикла в графе, основными из которых являются следующие теоремы.

Теорема 11. В Полном графе всегда существует гамильтонов цикл.

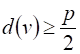Теорема 12. (Теорема Дирака.) Если любая из вершин графа с вершинами, имеет степень , то такой граф является гамильтоновым.

Задача о поиске гамильтонова цикла в графе имеет различные формулировки. Самой известной из них является «задача коммивояжера».

Пример. (Задача коммивояжера.) Имеется городов, расстояния между которыми известны. Требуется найти кратчайший путь, проходящий через все города и возвращающийся в исходный город.

Решение. Рассмотрим граф , моделирующий эту задачу. Множество вершин графа V интерпретируется как множество городов, . Множество ребер интерпретируется как множество дорог, соединяющих города, . Для ответа на вопрос задачи нужно найти в графе гамильтонов цикл наименьшей длины. При допущении, что любые два города соединяются дорогой, выполняются действия:

1) составляются все перестановки элементов множества V полного графа. Число таких перестановок при фиксированной вершине графа, из которой начинается обход, равно ;

2) вычисляется длина маршрута для каждой из перестановок первого действия;

3) выбирается перестановка наименьшей длины.

Эти действия составляют метод полного перебора. Даже при небольших значениях P для перебора всех гамильтоновых циклов графа требуются неоправданные затраты машинного времени и памяти. □

Задачи и упражнения

38. Найдите гамильтонов цикл в платоновом графе для тетраэдра и октаэдра (см. задачу 4.28).

39. Найдите значение , при котором граф является гамильтоновым графом.

40. Найдите значения и , при которых граф является гамильтоновым графом.

41. Найдите значение , при котором граф является гамильтоновым графом.

42. Найдите гамильтонов цикл в следующем графе:

43. Докажите, что в графе Петерсена, представленном на рис. 13, нет гамильтонова цикла.

< Предыдущая		Следующая >