09. Эйлеровы графы

Определение. Эйлеровым называется цикл в графе , содержащий Все ребра по Одному разу, а граф с таким циклом называется Эйлеровым.

Эйлеров граф является важной разновидностью Связного графа.

Теорема.9. Связный нетривиальный граф является эйлеровым тогда и только тогда, когда все вершины графа имеют Четную Степень.

Например, полный граф , представленный на рис. 4, является эйлеровым графом, потому что все его вершины имеют чётную степень.

Для построения эйлерова цикла в эйлеровом графе надо выполнить следующие действия:

1. Выйти из Любой вершины графа. Каждое пройденное ребро зачеркнуть или стереть. Стереть Изолированные вершины, которые при этом возникают. Этот путь обязательно замыкается в вершине выхода . Если путь проходит Все ребра графа, то путь является Эйлеровым циклом.

2. Если в графе остались ребра, не вошедшие в , то обязательно есть и вершина , инцидентная этим ребрам.

3. Новый путь начать в вершине . В новом пути использовать ребра, не вошедшие в . И этот путь обязательно завершится в вершине .

4. Объединить оба цикла и . Из вершины по пройти к вершине . Затем двигаться по пути . Вернувшись по этому пути к вершине , далее по оставшейся части пути возвратиться в вершину .

5. Если в графе остались ребра, не вошедшие в оба цикла и , то найти аналогично следующий цикл. Число вершин и ребер графа конечное, поэтому процесс построения циклов обязательно закончится.

Задачи и упражнения

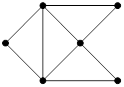
33. По нижеуказанной схеме улиц и перекрёстков составьте такой маршрут снегоуборочной машины, чтобы он начинался и заканчивался в одном и том же месте и проходил по каждой улице только один раз:

34. Найдите значение , при котором граф является эйлеровым графом.

35. Найдите значения и , при которых граф является эйлеровым графом.

36. Найдите значение , при котором граф является эйлеровым графом.

37. Найдите эйлеров цикл в графе:

< Предыдущая		Следующая >