08. Основные операции над графами

Определение. Дополнением графа называется такой граф , в котором две вершины смежны тогда и только тогда, когда они не смежны в .

Граф имеет те же вершины, что и граф . Граф имеет те и только те рёбра, которые добавляются в граф , чтобы он стал полным.

Например, на рис. 9 представлена диаграмма дополнения графа на рис. 1.

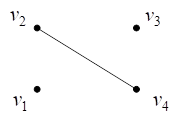
Рис. 9. Дополнение

Определение. Объединением графов и , не имеющих общих вершин и ребер, называется граф .

Граф содержит вершины и ребра, принадлежащие хотя бы одному из графов.

Например, на рис. 10 представлены диаграммы графов и и диаграмма их объединения .

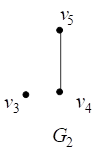
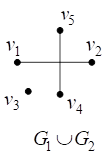
Рис. 10. Объединение графов

Определение. Соединением Графов и , не имеющих общих вершин и ребер, называется граф .

Граф соединения графов и содержит вершины и рёбра, принадлежащие хотя бы одному из графов и , и рёбра, соединяющие каждую вершину с каждой вершиной .

Например, на рис. 11 представлены диаграммы графов и и диаграмма их соединения .

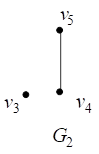
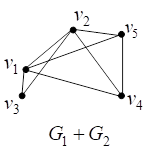
Рис. 11. Соединение графов

Определение. Удалением вершины графа называется операция, состоящая в удалении этой вершины Вместе с инцидентными ей ребрами.

Для обозначения удаления вершины графа используется символ .

Например, На рис. 12 представлен результат удаления вершины графа на рис. 1.

Рис. 12. Диаграмма графа

Определение. Удалением ребра графа называется операция удаления этого ребра при сохранении всех вершин графа.

Для обозначения удаления ребра графа используется символ .

Например, на рис. 13 представлен результат удаления ребра графа на рис. 1.

Рис. 13. Диаграмма графа

Определение. Добавлением новой вершины графа называется операция добавления этой вершины к множеству вершин , при сохранении всех ребер графа .

Для обозначения добавления новой вершины графа используется символ .

Например, на рис. 14 представлен результат добавления вершины графа на рис. 1.

Рис. 14. Диаграмма графа

Определение. Добавлением нового ребра графа называется операция добавления этого ребра к множеству ребер , при сохранении всех вершин .

Для обозначения добавления нового ребра графа используется символ .

Например, На рис. 15 представлен результат добавления ребра графа на рис. 1.

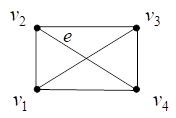
Рис. 15. Диаграмма графа

Определение. Стягиванием Подграфа графа называется операция, состоящая в следующем:

1) нахождение множества ;

2) нахождение множества ;

3) добавление к множеству новой вершины;

4) добавление к множеству новых ребер, инцидентных новой вершине и соединяющих новую вершину с оставшимися старыми вершинами.

Для обозначения стягивания подграфа графа используется символ .

Например, На рис. 16 представлены диаграммы графов и и диаграмма стягивания подграфа графа .

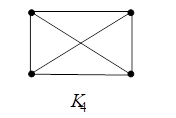
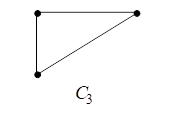
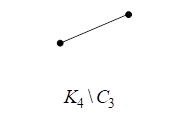
Рис. 16. Диаграмма графа

Определение. Размножением вершины графа называется операция, состоящая в следующем:

1) удаление из графа вершины вместе с инцидентными ей ребрами;

2) добавление пары новых вершин вместе с соединяющим их ребром;

3) соединение каждой из новых вершин с другими вершинами.

Для обозначения размножения вершины графа используется символ .

Например, На рис. 17 представлена диаграмма графа и диаграмма размножения его вершины.

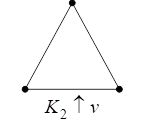
Рис. 17. Диаграмма графа

Задачи и упражнения

30. Определите типы графов на рис. 23 и на
рис. 24.

31. Графы и заданы диаграммами:

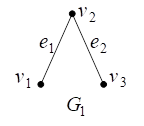
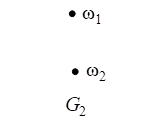
Постройте диаграммы следующих графов, являющихся результатами операций над графами и :

1) , ;

2) , , , ;

3) , , , ;

4) , , ;

5) , ;

6) , , , ;

7) , , , ;

8) , где , , Æ;

9) .

32. Постройте диаграммы следующих графов, являющихся результатами операций над графами и задачи 4.1: