07. Основные виды графов

Рассмотрим граф , Имеющий P вершин и Q ребер.

1. Пустой граф.

P Пустым называется граф, состоящий только из изолированных вершин.

В пустом графе , .

2. Тривиальный граф.

P Тривиальным называется граф, имеющий только одну вершину.

В тривиальном графе , .

3. Полный граф.

P Полным называется граф, каждая пара вершин которого является смежной.

Для обозначения полного графа используется специальный символ .

Например, на рис. 4 представлена диаграмма полного графа .

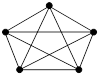
Рис. 4. Диаграмма полного графа

Из всех графов с P вершинами полный граф имеет наибольшее число ребер .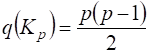

4. Двудольный граф.

P Двудольным называется граф, множество вершин которого разбивается на два Непересекающихся Подмножества V1 и V2 так, что Каждое ребро графа соединяет вершины из Разных подмножеств.

P Полным двудольным графом называется двудольный граф, в котором Каждая из M вершин множества V1 соединяется ребром с каждой из N вершин множества V2.

Например, граф задачи 4.6 является полным двудольным графом .

P Полный двудольный граф называется звездным или звездой.

Например, на рис. 5 представлена диаграмма звездного графа .

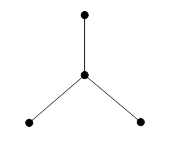
Рис. 5. Диаграмма звездного графа

5. Регулярный граф.

P Регулярным Степени K называется граф, все вершины которого имеют одну и ту же степень K.

Например, на рис. 6 представлена диаграмма графа Петерсена, который является регулярным графом третьей степени.

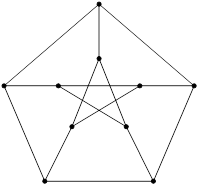
Рис. 6. Диаграмма графа Петерсена

6. Платонов граф.

P Платоновыми называются графы, образованные вершинами и ребрами пяти правильных многогранников – платоновых тел.

В табл. 1 приведены числовые характеристики правильных многогранников.

Таблица 1

Числовые характеристики правильных многогранников

Название Многогранника	Число граней	Вид Грани	Число вершин	Число ребер	Число ребер, примыкающих к одной Вершине
Тетраэдр	4	Правильный треугольник	4	6	3
Гексаэдр	6	Квадрат	8	12	3
Октаэдр	8	Правильный треугольник	6	12	4
Додекаэдр	12	Правильный пятиугольник	20	30	3
Икосаэдр	20	Правильный треугольник	12	30	5

Например, на рис. 7 представлена диаграмма платонова графа для гексаэдра.

Рис. 7. Диаграмма платонова графа для гексаэдра

Специальный символ используется для обозначения графа, состоящего из простого цикла с P вершинами.

Например, на рис. 8 представлена диаграмма простого цикла с тремя вершинами .

Рис. 8. Диаграмма простого цикла

Задачи и упражнения

22. Постройте диаграмму пустого графа, имеющего 3 вершины.

23. Докажите, что граф является регулярным. Сделайте вывод о степени регулярности полного графа .

24. Найдите в графе Петерсена циклы длиной 5 и 8. Вычислите цикломатическое число графа Петерсена.

25. Составьте матрицу смежности графа и укажите её характерную особенность.

26. Составьте матрицу смежности графа и укажите её характерную особенность.

27. Постройте диаграмму звездного графа .

28. Постройте платоновы графы для тетраэдра и октаэдра.

29. Всего в двух делегациях 20 человек. При встрече члены одной делегации обменялись рукопожатиями с членами другой. Найдите численный состав каждой делегации, если известно, что всего было сделано 96 рукопожатий.

Указание. Для решения задачи рассмотрите полный двудольный граф.

< Предыдущая		Следующая >