06. Связность графа
Определение. Связными называются такие две различные вершины графа, для которых существует соединяющая их цепь.
Определение. Связным Называется граф, все вершины которого связные.
Например, граф, диаграмма которого изображена на рис. 1, является связным, так как существует цепь, соединяющая его вершины, например, ![]() .
.
Теорема 4.7. Отношение связности вершин графа является отношением эквивалентности на множестве V.
Отношение связности вершин графа является разбиением множества V. Каждый класс эквивалентности называется Компонентой связности графа.
Определение. Числом связности ![]() графа называется число его различных компонент связности.
графа называется число его различных компонент связности.
Если ![]() , то граф G состоит из изолированных вершин.
, то граф G состоит из изолированных вершин.
Если ![]() , то граф G является связным.
, то граф G является связным.
Если ![]() , то граф G является несвязным.
, то граф G является несвязным.
Например, для графа на рис. 8 (см. пункт 4.1) ![]() .
.
Теорема 8. Для графа с P вершинами, Q ребрами и C Компонентами связности выполняется неравенство 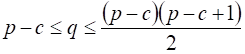 .
.
Определение. Цикломатическим числом графа ![]() с P вершинами, Q ребрами и C Компонентами связности называется неотрицательное число
с P вершинами, Q ребрами и C Компонентами связности называется неотрицательное число ![]() .
.
Цикломатическое число равно числу рёбер графа, после удаления которых получается граф без циклов.
Например, для графа на рис. 1 ![]() .
.
Задачи и упражнения
20. Определите числа связности и цикломатические числа графов задачи 4.1.
21. Докажите теорему 4.7.
| < Предыдущая | Следующая > |
|---|