11. Планарные графы

Уложенным На некоторой поверхности называется граф, который можно нарисовать на этой поверхности без пересекающихся ребер.

ОпреДеление. Плоским Называется граф, уложенный на плоскости.

Определение. Планарным Называется граф, изоморфный плоскому графу.

Например, граф, диаграмма которого изображена на рис. 1, является плоским графом.

Например, на рис. 18 представлен планарный граф и изоморфные ему плоские графы, составляющие укладку графа на плоскости.

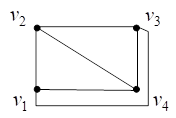
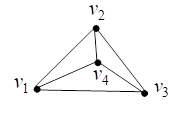
Рис. 18. Планарный граф и изоморфные ему плоские графы

Определение. Внутренней Гранью плоского графа называется множество точек плоскости, ограниченное простым циклом и не содержащее внутри него других циклов.

Определение. Внешней Гранью плоского графа называется множество точек плоскости без внутренних граней.

Число граней плоского графа обозначается символом .

Например, плоские графы на рис. 18 имеют по четыре грани, в том числе по три внутренние грани и по одной внешней.

Теорема 14. Для любого планарного графа , имеющего компонент связности, выполняется равенство

. (11.1)

Равенство (11.1) называется формулой связи числовых характеристик планарного графа. Для связного графа выполняется равенство

. (11.2)

Равенство (11.2) называется формулой Эйлера и является частным случаем формулы (11.1) при .

Теорема 15. Для любого связного планарного графа , имеющего Более трех вершин, выполняется неравенство

. (11.3)

Теорема 16. В любом планарном графе существует вершина, степень которой не превосходит пяти.

В дискретной математике существует несколько критериев планарности графа. Сформулированы алгоритмы, осуществляющие плоскую укладку планарного графа.

Теорема 17. Графы и не являются планарными.

Теорема 18. (Теорема Куратовского.) Граф планарен тогда и только тогда, когда он не имеет подграфов, стягивающихся к или к .

Пример. Есть три дома и три колодца. Требуется проложить дорожки от каждого дома к каждому колодцу так, чтобы они не пересекались.

Решение. Рассмотрим граф , моделирующий задачу. Множество вершин 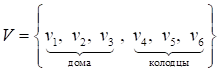, множество ребер , элементы которого соответствуют дорожкам. Граф является полным двудольным графом . Для ответа на вопрос задачи надо выполнить плоскую укладку графа . В 1930 году К. Куратовским доказано, что граф не является планарным. Значит, непересекающиеся дорожки проложить нельзя. □

Задачи и упражнения

44. Выполните плоскую укладку графа .

45. Проверьте выполнимость формулы Эйлера для графа .

46. Установите, является ли планарным регулярный граф пятой степени, имеющий 10 вершин.

47. Докажите, что граф , имеющий 11 вершин, и его дополнение не могут быть планарными одновременно.

48. В Бабаевском районе семь озёр, соединённых десятью каналами так, что от любого озера можно доплыть до любого другого. Сколько островов в Бабаевском районе?

< Предыдущая		Следующая >