20. Принцип сжимающих отображений.

Неподвижные точки нелинейного оператора.

Пусть нелинейный оператор действует из банахова пространства в , причём пересечения области определения и области значений непусто. Точка называется неподвижной точкой оператора , если .

Пусть дано некоторое множество из области определения

Определение. Будем говорить, что оператор является сжимающим на , если существует : .

Теорема 1. Пусть оператор отображает замкнутое в банаховом пространстве множество в себя и является на сжимающим оператором с коэффициентом сжатия . Тода в Оператор имеет единственную неподвижную точку и для произвольного последовательность : , сходится . Кроме того справедлива оценка скорости сходимости .

Доказательство.

Поскольку , то . Положим . Используя сжимаемость на , последовательно находим.

…………………………………………………….

Нужно показать, что фундаментальна.

Пользуясь неравенством треугольника и формулой суммы геометрической прогрессии:

Итак мы получили оценку . Отсюда вытекает фундаментальность , а вследствии полноты - сходимость к некоторому , а так как замкнуто, то . Докажем, что -неподвижная точка. Из условия сжимаемости на вытекает непрерывность на . Тогда переходя в равенстве к пределу получим . Докажем, что единственная неподвижная точка на . Пусть ещё одна точка, тогда И , вычитая и оценивая норму это неравенство возможно только если . Чтобы доказать оценку нужно перейти к пределу по в неравенстве .

Теорема 2. Пусть оператор отображает замкнутое в банаховом пространстве множество в себя и для некоторого является на сжимающим оператором. Тогда в Оператор имеет единственную неподвижную точку и для произвольного последовательность : , сходится .

Доказательство. Рассмотрим сжатие , по теореме 1 имеет единственную неподвижную точку : . Поскольку и перестановочны на , это означает, что , также является неподвижной точкой оператора , но в силу единственности этой точки .

Задача Коши для дифференциального уравнения в Банаховом пространстве.

Рассмотрим задачу

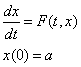
- нелинейный оператор двух переменных, вещественного переменного и переменного из банахова пространства.

Теорема 2. Пусть непрерывен по при каждом фиксированном и при и

Тогда на , где существует единственное решение задачи Коши.

Схема доказательства. Можно показать, что дифференциальное уравнение эквивалентно интегральному уравнению.

Далее необходимо показать, что в банаховом пространстве абстрактных, непрерывных на функций со значениями в и нормой в замкнутом шаре нелинейный оператор является сжимающим.

Замечание. Решение определено лишь на , а не на всём , пример , точное решение имеет вид , показывает, что в общем случае нельзя гарантировать существования на всем .

Теорема 3. . Пусть непрерывен по при каждом фиксированном и удовлетворяет условию Липшица, тогда при существует единственное решение задачи Коши.

Схема доказательства. Как и в предидущей теореме сводим задачу к эквивалентному интегральному уравнению, далее имеем оценку

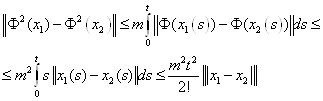
, поскольку при т. е - сжимающий.

Итерационный процесс Ньютона.

Пусть - нелинейный оператор, определенный в окрестности решения уравнения , непрерывно дифференцируеиый в в смысле Фреше. Пусть, далее, в оператор непрерывно обратим. Итерационный процесс Ньютона состоит в следующем. Выбирается начальное приближение и лежащее достаточно близко к решению . Дальнейшее приближение , ..вычисляются по формуле

Существуют различные варианты теорем о сходимости этого итерационного процесса. Приведём один из вариантов, где существование решения не предполагается, а доказывается.

Теорема. Пусть в шаре оператор дифференцируем и его производная удовлетворяет условию Липшица с постоянной . Пусть, далее в оператор непрерывно обратим и существует постоянная такая, что ,

Пусть далее, . Тогда, если и , то уравнение имеет решение , к которому сходится итерационный процесс Ньютона, начатый с . Скорость сходимости к даётся неравенством

Доказательство. Введём обозначения , , , .

Итерационный процесс Ньютона в этих обозначениях записывается так:

Покажем сначала, что . и следовательно, , тюе ,

Далее, , поэтому

Учитывая то, что производная удовлетворяет условию Липшица.

.

Дальнейшие рассуждения проводим методом полной математической индукции.

Пусть уже доказано, что и что справедливы

Покажем, что

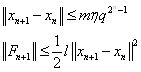
Действительно

Далее, имеем

Это позволяет оценить :

Учитывая то, что производная удовлетворяет условию Липшица.

.

Установим фундаментальность . Из неравенства треугольника и полученных оценок имеем

Отсюда при равномерно по , так как ряд . Итак, - фундаментальна, а значит в силу полноты сходящаяся. Обозначим через её предел. Вследствие замкнутости . Докажем, что - решение уравнения . Для этого достаточно перейти к пределу в выражении.

Тогда

Отсюда , так как - обратим.

Далее так как

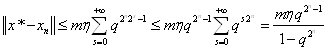
Модифицированный метод Ньютона.

Преимущество в том, что обратный оператор вычисляется только один раз, недостаток - ухудшается скорость сходимости.

< Предыдущая		Следующая >