18. Нелинейные операторы.

Производная Фреше нелинейного оператора. Рассмотрим нелинейный оператор с областью определения в банаховом пространстве и со значениями в банаховом пространстве . Предположим, что оператор определён в некоторой окрестности точки .

Определение. Оператор называется дифференцируемым в точке (в смысле Фреше), если существует линейный ограниченный оператор , такой, что для любых

Оператор называется производной (Фреше) оператора в точке и обозначается или . Можно записать в виде ,

Где , при .

Определение. Если оператор дифференцируем в точке , то выражение

Называется дифференциалом Фреше, т. е дифференциал это значение на элементе .

Свойства.

1. 

2. 

3.  ,

Пример.

Производная нелинейного оператора в конечномерном случае.

: , т. е

, ,..,

Производная Фреше это матрица Якоби (матрица первых производных). Производная суперпозиции получается как произведение матриц.

Формула конечных приращений Лагранжа.

Теорема. Пусть оператор непрерывно дифференцируемый в окрестности точки , тогда в справедлива формула Лагранжа:

Доказательство. По формуле дифференцирования суперпозиции

Интегрируя это тождество от 0 до 1, получим искомую формулу.

Определение. Будем говорить, что удовлетворяет на условию Липшица (с постоянной ), если :

Лемма 1. Пусть непрерывно диффренцируемый на выпуклом множестве , причём на , тода удовлетворяет на условию Липшица с постоянной Липшица .

Доказательство.

Оценим норму

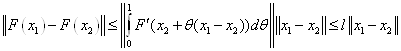
Лемма 2. Пусть непрерывнодифференцируем на выпуклом множестве , причём

, тогда справедлива оценка

Доказательство.

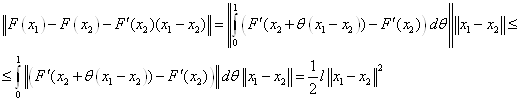
< Предыдущая		Следующая >