17. Прямое произведение.
Прямое произведение
![]()
Оказывается прямое произведение коммутативно, т. е. ![]() , доказательство см. «Владимиров».
, доказательство см. «Владимиров».
Сверткой двух обобщённых функций называется функционал
![]()
Свёртка существует не всегда, т. к. ![]() .
.
Теорема. Если свёртка ![]() существует, то существует свёртки
существует, то существует свёртки ![]() и
и ![]() , причём
, причём
![]() .
.
Отсюда в частности вытекает, что ![]() .
.
Отметим, что существование свёрток ![]() и
и ![]() не достаточно для существования свёртки
не достаточно для существования свёртки ![]() , в частности эти свёртки не обязаны быть равными.
, в частности эти свёртки не обязаны быть равными.
![]() , но
, но ![]()
Важнейшим приложением обобщённых функций является построение фундаментального решения дифференциального оператора.
![]() в
в ![]() .
.
![]()
Здесь ![]() - целочисленный вектор с неотрицательными составляющими
- целочисленный вектор с неотрицательными составляющими ![]() . Через
. Через ![]() порядка
порядка ![]() .
.
![]() ,
, ![]() , также используют следующие сокращённые обозначения.
, также используют следующие сокращённые обозначения.
![]()
![]()
Лемма. Для того чтобы обобщённая функция была решением оператора ![]() , необходимо и достаточно, чтобы её преобразование Фурье
, необходимо и достаточно, чтобы её преобразование Фурье ![]() удовлетворяло уравнению.
удовлетворяло уравнению.
![]() .
.
Доказательство. Пусть ![]() фундаментальное решение оператора
фундаментальное решение оператора ![]() к обеим частям равенства, получим.
к обеим частям равенства, получим.
![]()

Таким образом доказанная лемма сводит задачу построения фундаментальных решений дифференциальных операторов с постоянными коэффициентами к решению в ![]() алгебраических уравнений вида
алгебраических уравнений вида ![]() . Решение такой задачи может быть не единственно, например, различными решениями уравнения
. Решение такой задачи может быть не единственно, например, различными решениями уравнения ![]() являются обобщённые функции
являются обобщённые функции ![]() и
и ![]() .
.
Если функция ![]() локально интегрируема в
локально интегрируема в ![]() , то она (определяемый ею регулярный функционал) является решением в
, то она (определяемый ею регулярный функционал) является решением в ![]() уравнения (9). Если же функция
уравнения (9). Если же функция ![]() , то возникает нетривиальная задача о построении в
, то возникает нетривиальная задача о построении в ![]() решения уравнения
решения уравнения ![]() . Хёрмандером доказано, что уравнение всегда разрешимо в
. Хёрмандером доказано, что уравнение всегда разрешимо в ![]() .
.
С помощью фундаментального решения ![]() оператора
оператора ![]() можно построить решение уравнения
можно построить решение уравнения ![]() с произвольной правой частью.
с произвольной правой частью.
Теорема. Пусть ![]() такова, что свёртка
такова, что свёртка ![]() существует в
существует в ![]() . Тогда решение уравнения
. Тогда решение уравнения ![]() существует и даётся формулой:
существует и даётся формулой: ![]() .
.
Это решение единственно в классе тех обобщённых функций из ![]() , для которых существует свёртка.
, для которых существует свёртка.
Доказательство. Пользуясь формулой дифференцирования свёртки.
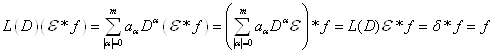
Докажем единственность, для этого достаточно установить, что соответствующее однородное уравнение ![]() .
.
![]()
Примеры.
1. Пусть функция ![]() такова, что
такова, что ![]() и
и ![]() . Покажем, что
. Покажем, что ![]() , где обозначено
, где обозначено ![]()
Действительно, если ![]() , то
, то

Если же функция ![]() имеет изолированные разрывы первого рода в точках
имеет изолированные разрывы первого рода в точках ![]() , тогда
, тогда
![]() .
.
2. Проверим, что функция ![]() , где
, где ![]() есть решение однородного дифференциального уравнения
есть решение однородного дифференциального уравнения
![]() , удовлетворяющее условиям
, удовлетворяющее условиям ![]() ,
, ![]() , удовлетворяет условию
, удовлетворяет условию ![]()
Действительно, пользуясь формулой полученной в предыдущем примере, получаем 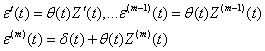
Отсюда ![]()
В частности ![]() ,
, ![]() являются фундаментальными решениями операторов
являются фундаментальными решениями операторов ![]() и
и ![]()
Фундаментальное решение оператора теплопроводности.
![]()
Выведем формулу для фундаментального решения, используя преобразование Фурье.
![]()
![]()
![]()
В результате для обобщённой функции ![]()
Получаем уравнение ![]()
Пользуясь формулой из предыдущего примера
![]()
Отсюда применяя обратное преобразование Фурье.

| < Предыдущая | Следующая > |
|---|