16. Обобщённые функции.
В основе теории лежит пространство ![]() . Каждая функция
. Каждая функция ![]() обладает следующими свойствами.
обладает следующими свойствами.
1) ![]() непрерывная на оси
непрерывная на оси ![]() бесконечно дифференцируемая функция.
бесконечно дифференцируемая функция.
2) Для любого неотрицательного целого числа ![]() и любого многочлена
и любого многочлена ![]() произвольной степени
произвольной степени ![]() :
: ![]() .
.
Из этих свойств вытекает, что для каждой функции ![]() существует конечный несобственный интеграл.
существует конечный несобственный интеграл. ![]()
Тем самым, каждая ![]() вместе со своими производными принадлежит
вместе со своими производными принадлежит ![]() .
.
Примером функции ![]() Является
Является ![]() . По индукции нетрудно показать, что
. По индукции нетрудно показать, что ![]() . Очевидно свойства 1)-2) выполняются.
. Очевидно свойства 1)-2) выполняются.
Вторым примером функции ![]() является так называемая финитная функция. Это бесконечно дифференцируемая, равная нулю вне некоторого отрезка
является так называемая финитная функция. Это бесконечно дифференцируемая, равная нулю вне некоторого отрезка ![]() функция. Любая её производная тоже равна нулю вне некоторого отрезка. Поэтому свойства 1)-2) очевидно выполнены.
функция. Любая её производная тоже равна нулю вне некоторого отрезка. Поэтому свойства 1)-2) очевидно выполнены.
На множестве ![]() вводится понятие предельного перехода. Последовательность
вводится понятие предельного перехода. Последовательность ![]()
![]() называется сходящейся к функции
называется сходящейся к функции ![]() , если для любого неотрицательного целого числа
, если для любого неотрицательного целого числа ![]() и любого многочлена
и любого многочлена ![]() имеет место равенство.
имеет место равенство.
![]()
Равномерно относительно всех ![]() .
.
![]() является линейным пространством.
является линейным пространством.
Напомним, что на ![]() задан функционал, если для каждой
задан функционал, если для каждой ![]() задано число
задано число ![]() :
: ![]() . Функционал называется линейным, если
. Функционал называется линейным, если ![]() , непрерывным, если
, непрерывным, если ![]()
Линейный непрерывный функционал, определённый на ![]() называется обобщённой функцией. Совокупность всех обобщённых функций над
называется обобщённой функцией. Совокупность всех обобщённых функций над ![]() обозначается через
обозначается через ![]() . Приведём примеры.
. Приведём примеры.
Пусть ![]() кусочно-непрерывная функция, удовлетворяющая неравенству
кусочно-непрерывная функция, удовлетворяющая неравенству
![]() .
.
![]()
Линейность и непрерывность очевидна.
Теорема. Для того чтобы две кусочно-непрерывные функции, предстовляли равные обобщённые функции, необходимо и достаточно чтобы они были равны в точках непрерывености.
Поэтому обобщённую функцию, представимую через интеграл от кусочно-непрерывную функцию ![]() отождествляют с этой функцией.
отождествляют с этой функцией.
Замечание. Существуют функции, например ![]() , для которых интеграл не является обобщённой функцией. Обобщённые функции, порождённые обычными функциями называются регулярными, однако есть и нерегулярные, например
, для которых интеграл не является обобщённой функцией. Обобщённые функции, порождённые обычными функциями называются регулярными, однако есть и нерегулярные, например ![]() :
: ![]() .
.
Формулы Сохоцкого.
Введём линейный функционал.
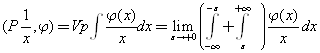
Справедливы формулы Сохоцкого.
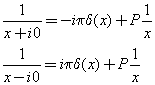
Здесь
![]()
Операции над обобщёнными функциями.
Пусть ![]() - обычная функция
- обычная функция
![]()
Это определение мы и примем за определение производной обобщённой функции., т. е ![]()
![]()
![]() .
.
Очевидно любая обобщённая функция имеет производную какого угодно порядка.
![]()
Например, ![]()
![]() , где
, где ![]() - функция Хевисайда.
- функция Хевисайда.
По определению последовательность обобщённых функций ![]() сходится к
сходится к ![]() , если
, если ![]()
![]() .
.
А это означает, что можно рассматривать ряды состоящие из обобщённых функций. Для обобщённых функций вводится операция умножения на бесконечно дифференцируемую функцию. С помощью равенства.
![]() .
.
Однако Шварцем показано, что произведение двух обобщённых функций, которое было бы ассоциативно и коммутативно определить нельзя. Действительно тогда бы мы имели противоречивую цепочку равенств.
![]()
Отметим, что если ![]() ,
, ![]() действительное число, то обобщённые функции
действительное число, то обобщённые функции ![]() определяются при помощи равенств.
определяются при помощи равенств.
![]()
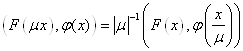
Эти определения естественны так как они автоматически выполнены для регулярных обобщённых функций.
Преобразование Фурье обобщённых функций.
Отметим, что если функция ![]() , то её преобразование Фурье
, то её преобразование Фурье
![]()
![]()
также принадлежит ![]() .
.
При этом это преобразование отображает ![]() на
на ![]() линейно и непрерывно.
линейно и непрерывно.
Непрерывность заключается в том, что если какая-либо последовательность функций ![]() сходится в смысле
сходится в смысле ![]() к функции
к функции ![]() , то и
, то и ![]() сходится к
сходится к ![]() в смысле сходимости в
в смысле сходимости в ![]() . То же самое справедливо и для обратного преобразования Фурье
. То же самое справедливо и для обратного преобразования Фурье
![]() .
.
После сделанных замечаний естественно определить преобразование Фурье для обобщённых функций
![]() . Откуда сразу немедленно следует
. Откуда сразу немедленно следует ![]() .
.
Отметим также, ![]()
![]()
Для обобщённых функций имеет место тот же факт
![]()
По индукции легко выводим ![]()
Пример. Найти преобразование Фурье для обобщённой функции.
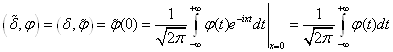
Т. е. ![]()
Преобразование Фурье обобщённых функций обладает свойствами преобразований Фурье обычных функций. ![]()
![]() .
.
.
| < Предыдущая | Следующая > |
|---|