15. Вариационные задачи с подвижными границами.
Предположим, что одна или более граничных точек может перемещаться.
Если на какой-нибудь кривой ![]() достигается экстремум в задаче с подвижными граничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой
достигается экстремум в задаче с подвижными граничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой ![]() . Таким образом,
. Таким образом, ![]() должна удовлетворять уравнению Эйлера.
должна удовлетворять уравнению Эйлера. ![]() . Решение этого уравнения содержит произвольные постоянные, которые определялись из граничных условий в задачах с неподвижными границами. В случае подвижных границ они определяются из равенства нулю функционала.
. Решение этого уравнения содержит произвольные постоянные, которые определялись из граничных условий в задачах с неподвижными границами. В случае подвижных границ они определяются из равенства нулю функционала.
Пусть ![]() закреплены, тогда найдём вариацию функционала
закреплены, тогда найдём вариацию функционала ![]() . Допустимые кривые будем считать близкими, если модули вариаций
. Допустимые кривые будем считать близкими, если модули вариаций ![]() и
и ![]() малы и малы модули приращений
малы и малы модули приращений ![]() .
.
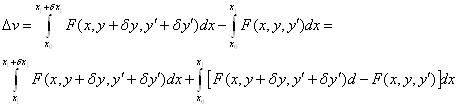
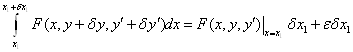
![]()
Второе слагаемое по формуле Тейлора.


Так как ![]() закреплена, то нижняя подстановка обращается в ноль.
закреплена, то нижняя подстановка обращается в ноль. ![]() !
!
![]()
![]()
Если приращения независимы, то отсюда следует. Что
![]() и
и ![]()
Но чаще приходится рассматривать случай, когда вариации ![]() и
и ![]() зависимы
зависимы ![]() .
.
![]() условие транверсальности.
условие транверсальности.
Пример найти условие трансверсальности для функционалов вида
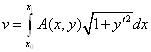
![]()
Или
![]()
Т. е ![]() условие ортогональности.
условие ортогональности.
![]() ,
, ![]()
Интегральными кривыми являются окружности ![]() . Первое граничное условие даёт
. Первое граничное условие даёт ![]() . Так как условие трансверсальности для данного функционала сводится, условию ортогональности
. Так как условие трансверсальности для данного функционала сводится, условию ортогональности ![]() т. е.
т. е. ![]()
![]()
Если граничная точка ![]() может перемещаться лишь по вертикальной прямой, то
может перемещаться лишь по вертикальной прямой, то ![]() и
и ![]()
Вариационные задачи на условный экстремум.
Найти экстремум функционала 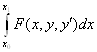 при условии
при условии ![]() ,
, ![]()
 . Здесь также можно доказать справедливость метода неопределённых множителей Лагранжа.
. Здесь также можно доказать справедливость метода неопределённых множителей Лагранжа.
Составим функцию Лагранжа ![]() для неё записываем уравнение Эйлера.
для неё записываем уравнение Эйлера.
Неизвестные ![]() находим из условий связи.
находим из условий связи.
Пример. Найти кривую ![]() , заданной длины
, заданной длины ![]() , для которой площадь
, для которой площадь ![]() Под ней достигает максимума.
Под ней достигает максимума.
 ,
, ![]()
При изопериметрическом условии 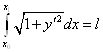
![]() не зависит от
не зависит от ![]() , поэтому уравнение Эйлера имеет первый интеграл
, поэтому уравнение Эйлера имеет первый интеграл ![]()
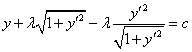
![]() вводя параметр
вводя параметр ![]() , полагая
, полагая ![]() , тогда получим
, тогда получим
![]() , откуда
, откуда ![]()
![]() ,
, ![]() ,
,
Получим семейство окружностей ![]()
Константы определяются из условия ![]() ,
, ![]() .
.
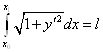
Задача о максимальной площади между двумя кривыми.
Найти экстремаль ![]()
![]() ,
, ![]() и интегральной связи
и интегральной связи ![]()
![]() уравнение Эйлера
уравнение Эйлера ![]()
![]() =
=![]() .
.
| < Предыдущая | Следующая > |
|---|