14. Примеры.

Задача о наименьшей поверхности вращения.

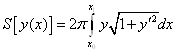
Подынтегральная функция не зависит от .

В данном случае:

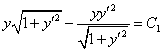
После упрощений

Интегрируется подстановкой , тогда

Исключая , будем иметь - семейство цепных линий, от вращения которых образуются каноиды.

Задача о брахистохроне.

,

Подынтегральная функция не зависит от .

После упрощений

или

Введём параметр

- радиус крутящегося круга.

Функционалы, зависящие от производной более высокого порядка

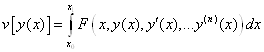
Пример. Найти экстремаль функционала

, т. е. , с учётом гр. усл. .

Достаточное условие экстремума.

Условие Якоби.

Центральным полем экстремалей, называется семейство экстремалей, которые покрывают некоторую область и нигде не пересекаются в этой области, кроме центра.

Нетрудно получить аналитическое условие включения экстремали в центральное поле экстремалей.

(1)

Выражения вычисляются на конкретной экстремали и являются конкретными функциями

Экстремаль может быть включена в поле экстремалей, если уравнение (1) имеет не тривиальное решение удовлетворяющее и не обращающееся в ноль нигде при .

Замечание. Можно показать, что условие Якоби необходимо для достижения экстремума.

Предположим, что условие Якоби выполнено, это означает, что в каждой точке определён наклон центрального поля равный . Для определения знака приращения при переходе на близкую кривую, преобразуем приращение

к более удобному виду. Для этого Рассмотрим вспомогательный функционал

(2) на экстремали он совпадает с . Но с другой стороны, если мы введём функцию в которую превращается функционал на экстремалях поля, то дифференциал в точности совпадает с подынтегральным выражением для (2), то есть (2) не зависит от пути интегрирования соединяющий две фиксированные точки, поэтому = .

То есть

=

=

Функция называется функцией Вейерштрасса.

Достаточным, для достижения функционалом экстремума будут следующие условия.

Для слабого экстремума.

1.  Кривая С является экстремалью, удовлетворяющей граничным условиям.

2.  Экстремаль С может быть включена в поле экстремалей, это условие можно заменить, на условие Якоби.

3.  Функция не меняет знака во всех точках , близких к С и для всех близких к . Для минимума , в случае максимума .

Для сильного экстремума

1.  Кривая С является экстремалью, удовлетворяющей граничным условиям.

2.  Экстремаль С может быть включена в поле экстремалей, это условие можно заменить, на условие Якоби.

3.  Функция не меняет знака во всех точках , и для произвольных . Для минимума , в случае максимума .

Пример. Исследовать на экстремум функционал.

Экстремалями являются прямые линии.

Пучок прямых образует центральное поле включающее .

на экстремали и все условия слабого минимума выполнены.

Если же любое, то условия не выполнены и сильный минимум не достигается.

Функция

При исследовании на слабый экстремум должна сохранять знак вблизи экстремали и для близких к , а на самом деле на самой экстремали, тогда в силу непрерывности будет и вблизи.

При исследовании на слабый экстремум должна сохранять знак вблизи экстремали и для любых

Это условие носит название условие Лежандра.

< Предыдущая		Следующая >