13. Уравнение Эйлера
Исследуем на экстремум функционал 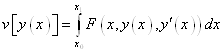 .
.
Граничные точки допустимых кривых закреплены: Y(x0)=y0, y(x1)=y1.
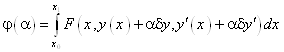

Интегрируя по частям получим
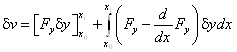
Но ![]() , поэтому необходимое условие экстремума:
, поэтому необходимое условие экстремума:

Основная лемма вариационного исчисления.
Если для каждой непрерывной функции h(X)
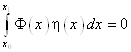
Где функция F(X) непрерывна на отрезке [X0,X1], то F(X)º0.
Доказательство. От противного. Если существует точка где F(X)¹0, то она в силу непрерывности сохраняет знак в некоторой окрестности этой точки, выберем h(X) так, чтобы она тоже сохраняла знак в этой окрестности, а в остальных точках равна нулю, тогда очевидно  .
.
Применим лемму для упрощения необходимого условия
![]() или
или ![]()
Замечание. Краевая задача
![]() , Y(x0)=y0, y(x1)=y1.
, Y(x0)=y0, y(x1)=y1.
Не всегда имеет решение, причём может иметь и не единственное решение.
Пример. На каких кривых может достигать экстремума функционал
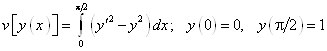
Уравнение Эйлера имеет вид: Y”+y=0.
Y=C1Cosx+C2Sinx. Из граничных условий Y=sinx.
Рассмотрим некоторые простейшие случаи интегрирования уравнения Эйлера.
1. F Не зависит от Y’: Fy(x, y)=0 кривая не содержит элементов произвола и лишь в исключительных случаях удовлетворяет граничным условиям.
2. F Линейно зависит от Y’: F=M(x, y)+N(x, y)y’
Уравнение Эйлера:
![]()
Или
My-Nx=0.
Как и предыдущем случае кривая вообще говоря не удовлетворяет граничным условиям, если же My-Nxº0, то Mdx+Ndy - полный дифференциал и интеграл не зависит от пути интегрирования, то есть вариационная задача теряет смысл.
3. F Зависит лишь от Y’: F=F(y’), уравнение Эйлера Fyyy’’=0
Y=C1X+C2.
4. F Зависит лишь от X И Y’. уравнение Эйлера ![]() , может быть проинтегрировано Fy(x, y’)=C1
, может быть проинтегрировано Fy(x, y’)=C1
Полученное уравнение первого порядка не содержит Y, а следовательно может быть проинтегрировано, например с помощью введения параметра.
5. F Зависит лишь от Y И Y’.
Ур-е Эйлера Fy-Fyyy’-Fyyy’’=0, если домножить на Y’ свернётся в полную производную ![]() , интегрируя (F-y’Fy)=C1. Это уравнение не содержит X И может быть проинтегрировано методом разделения переменных или введения параметра.
, интегрируя (F-y’Fy)=C1. Это уравнение не содержит X И может быть проинтегрировано методом разделения переменных или введения параметра.
| < Предыдущая | Следующая > |
|---|