10. Теорема Гильберта-Шмидта.

Определение. Непрерывная функция представима через ядро , если существует непрерывная на функция , т. е .

Теорема. Если представима через симметричное ядро , то она может быть разложена в ряд по с. ф

, где , причём ряд сходится абсолютно и равномерно.

Доказательство. Покажем, что ряд сходится равномерно

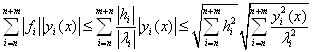
Заметим, что , величина коэф. Фурье функции при каждом фиксированном , рассматриваемого как функция .

Воспользуемся теперь неравенством Бесселя для и ,

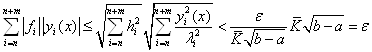
Ряд из непрерывных функций сходится равномерно к некоторой непрерывной функции , а, следовательно, осталось доказать

Обозначим . Покажем, что , ортогонально всем , в силу равномерной сходимости его можно почленно интегрировать

.

Следовательно, по теореме из прошлой лекции , но

А, следовательно, , т. е .

Повторные ядра.

Рассмотрим

Получим для

Т. е.

Теорема. Для повторных ядер справедливо соотношение

Доказательство. По индукции.

Теорема. Если ядро такое, что - вещественная непрерывная по совокупности переменных функция, , то этими же свойствами обладает повторные ядра любого порядка.

Последняя формула показывает, что повторное ядро представимо через ядро , роль функции играет .

Выражение для коэффициентов Фурье.

Т. е

Теорема. При справедливо разложение

(1) причём ряд сходится абсолютно и равномерно.

Определение. Ядро называется положительно определённым, если все его собственные значения .

Теорема Мерсера. Для положительно определённого ядра справедливо равенство (1) причём ряд сходится абсолютно и равномерно.

Замечание. Теорема остаётся справедливой и если у ядра конечное число отрицательных собственных значений.

Ослабление требований на ядро.

1.  Можно рассматривать всю эту теорию пространстве с комплексным скалярным произведением. Роль симметричных операторов играют эрмитовы, для которых . И получить аналогичные результаты, в частности , и доказательство действительности .

2.  Все полученные результаты устанавливаются аналогично, когда в интегральном уравнении интегралы являются многократными, а вместо фигурируют координаты точек пространства.

3.  Требование непрерывности можно ослабить а именно. Результаты относящиеся к существованию с. з. справедливы и для полярных ядер:

, Размерность пространства, расстояние между точками в -мерном пространстве. Теорема Гильберта-Шмидта и следствия из неё справедлива для слабополярных ядер

4.  Требование симметрии или эрмитовости снять нельзя придоказательстве существования собственных значений

Пример. .

< Предыдущая		Следующая >