09. Существование собственных векторов вполне непрерывного симметричного оператора.

Теорема. симметричный вполне непрерывный оператор обладает собственным вектором, которому отвечает собственное значение .

Случай очевиден.

Пусть

Лемма1. Для всякого симметричного оператора и любого единичного вектора справедливо.

Причём равенство имеет место тогда и только когда собственный вектор оператора с собственным значением .

Доказательство.

Пусть имеет место равенство, тогда , это неравенство Коши-Буняковского. Равенство возможно только если вектора , но тогда

Обратно, пусть , тогда .

Определение. Назовём максимальным вектором оператора , такой единичный вектор , на котором , т. е достигается .

Лемма2. Симметричный вполне непрерывный оператор обладает максимальным вектором.

Пусть , рассмотрим все . . Это значит, что найдётся , , при . Из этой последовательности в силу полной непрерывности можно выбрать сходящуюся подпоследовательность к некоторому элементу , причём , а, следовательно, . Положим , -единичный вектор, покажем, что он является максимальным, т. е. . Построим последовательность . При этом будем иметь , но по лемме 1

Но

Таким образом с одной стороны

, с другой перейдём к пределу (это можно сделать в силу непрерывности, которая следует из полной непрерывности)

, т. е

Лемма 3. Максимальный вектор симметричного оператора является собственным вектором с собственным значением .

Доказательство. По предыдущей лемме и по лемме 1

В силу равенства крайних членов этой цепочки имеем , но тогда по лемме 1, является собственным вектором оператора , с с. з. , т. е , что и требовалось.

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ.

Имеем или или . Пусть вектор , тогда , , т. е. собственный вектор, а собственное значение. Если , то и собственный вектор, а собственное значение.

Замечание. Если оставить только требование симметрии и не требовать полной непрерывности, то оператор может и не иметь собственных векторов.

, этот оператор является симметричным

. Однако очевидно, что не при каком не выполнено .

Существование последовательности собственных векторов.

Пусть пространство , в котором было доказано существование с. з. и с. в. обозначим . Построим подпространство , элементы которого выделены условием , оно называется ортогональным . Ведённое подпространство обладает следующими свойствами.

1.  является подпространством, инвариантным относительно оператора , т. е. если , то и

2.  является подпространством, замкнутым относительно предельного перехода, т. е если и , то

Докажем. 1.

Докажем 2

Но левая часть не зависит от значит в точности равно нулю.

Свойства 1-2 позволяют для провести те же рассуждения, что и для и тогда существует последовательность собственных векторов и собственных значений .Процесс может оборваться, если на каком-то этапе для любого

Свойства собственных векторов и собственных значений вполненепрерывного симметричного оператора.

1.  Собственые вектора, отвечающие различным собственным значениям, ортогональны между собой.

Доказательство . В силу симметрии оператора левая часть равна нулю, следовательно,

2.  Имеется не более конечного числа линейно независимых собственных векторов, для которых , для любого наперёд заданного .

3.  Каждому отличному от нуля собственному значению отвечает лишь конечное число линейно независимых векторов, это число называется рангом собств. значения.

4.  Для того чтобы вектор удовлетворял уравнению , необходимо и достаточно, чтобы он был ортогонален всем собственным векторам оператора с отличными от нуля собственными значениями.

Доказательство. Необходимость. Пусть

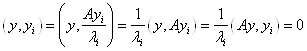
Достаточность. Предположим противное, т. е. допустим, что , а , т. е. . Пусть , .Рассмотрим все собственные вектора для которых , таких векторов конечное число . Рассмотрим подпространство . , с другой стороны и . Противоречие.

Однородные уравнения Фредгольма второго рода.

Будем считать, что - вещественная непрерывная по совокупности переменных функция,

Теорема. Если - собственная функция ядра , а - соответствующее собственное значение, то ядро имеет те же с. з и с. ф., что и ядро , кроме и .

Следствие. Если, , .. - собственные функции ядра , а , , …Соответствующее собственное значение, то ядро имеет те же с. з и с. ф., что и ядро , кроме , , .. и , , ….

Вырожденные ядра.

Определение. Ядро , представимое конечной суммой вида

Называется вырожденным.

Теорема.

1. Вырожденное ядро имеет конечное число собственных значений (в том числе может и не иметь).

2. Если симметричное ядро имеет конечное число собственных значений, то оно вырождено.

Доказательство. 1.

Где , тогда

В результате пришли к системе однородных алгебраических уравнений Если , то система имеет не тривиальные решения.

2.Рассмотрим ядро , у этого ядра есть собственная функция , ортогональная всем предыдущим, сдругой стороны , т. к. по условию эти n функций исчерпывают все линейно независимые с. ф., помножим скалярно на , получим, что

< Предыдущая		Следующая >