08. Интегральные уравнения.

Интегральным уравнением называется уравнение, содержащее неизвестную функцию под знаком интеграла. Например.

, где - заданные функции.

- неизвестная функция.

Вполне непрерывные операторы в бесконечномерном евклидовом пространстве.

Здесь и далее будем рассматривать пространство непрерывных функций заданных на сегменте , со скалярным произведением

Пусть . Зададим функцию непрерывную по совокупности переменных при . Определим оператор (т. е. функции , поставим в соответствие функцию следующим образом:

Определение. называется собственным вектором оператора , если , - собственное значение.

Теорема. Если непрерывная по совокупности переменных, то оператор фредгольма является ограниченным.

Доказательство. Неравенство Коши-Буняковского.

Пример неограниченного оператора оператор дифференцирования

.

Определение. Если существует не зависящая от константа : , то последовательность называется ограниченной.

Определение. Последовательность будем называть компактной в , если из любого бесконечного множества её элементов можно выделить подпоследовательность элементов, сходящуюся к некоторому элементу

Определение. Оператор называется вполне непрерывным в , если, какова бы не была ограниченная последовательность из неё всегда, соответствующая последовательность является компактной.

Теорема. Вполне непрерывный оператор является ограниченным.

Доказательство. От противного. Пусть не является ограниченным. Тогда существует последовательность , такая что , а . В силу полной непрерывности из последовательности , можно выделить сходящуюся подпоследовательность . С одной стороны , с другой стороны .Противоречие.

Следствие. Вполне непрерывный оператор является непрерывным.

Замечание. Обратное утверждение не верно. Например единичный оператор. Рассмотрим последовательность

.

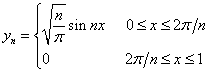
Предположим, что существует подпоследовательность сходящаяся в среднем к некоторой непрерывной функции, тогда для любого

Но

Здесь первое слагаемое, начиная с некоторого достаточно большого равно единице, а второе и третье стремятся вместе с к нулю. Противоречие.

Вспомним матанализ!

Мы знаем, что каждая ограниченная числовая последовательность содержит сходящуюся подпоследовательность. Верно ли подобное утверждение для функций.

Определение. Будем говорить, что последовательность Равномерно ограниченна На множестве , если существует такое , что .

Мы можем добиться, что подпоследовательность будет сходиться поточечно в каждой точке счётного всюду плотного подмножества . Однако, даже если Равномерно ограниченна, Не обязательно существует подпоследовательность сходящаяся поточечно на . Следующий пример иллюстрирует этот факт.

Пример. Пусть , Допусти существует строго возрастающая последовательность , такая, что последовательность сходится при каждом . Тогда

,

Значит

По теореме Лебега об интегрировании ограниченно сходящихся последовательностей

Однако непосредственные вычисления дают

Другой вопрос: вякая ли сходящаяся последовательность содержит равномерно сходящуюся?

Пример. Пусть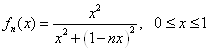

Тогда , т. е. последовательность равномерно ограниченна. Более того , но , так что никакая подпоследовательность не сходится к нулю равномерно.

Теорема Арцела.

Определение. Последовательность называется равностепенно непрерывной на множестве , если , такое что

Следующая теорема справедлива на любом компакте, но нам она понадобится на отрезке.

Теорема.

1.  Если - равномерно сходящаяся последовательность функций, непрерывных на , то равностепенно непрерывна на .

2.  Если равномерно ограниченна и равностепенно непрерывна на , то содержит равномерно сходящуюся подпоследовательность.

Доказательство. Пусть выполнено 1. и такие что

Кроме того будет выполнено

Здесь использовалось, что непрерывная функция равномерно непрерывна на отрезке. Итак

Если и , то

Тем самым утверждение 1 доказано

Докажем утверждение 2. Пусть пронумерованные рациональные точки отрезка .

Ввиду того, что ограниченна, существует такая, что последовательность сходится. Рассмотрим теперь последовательности

Эти последовательности обладают следующими свойствами.

1.  бесконечная подпоследовательность последовательности

2.  сходится при

Теперь спустимся по диагонали

Последовательность за исключением, быть может, первых членов подпоследовательность , значит, сходится при каждом .

Пусть . Ввиду того что последовательность равностепенно непрерывна, существует что если , то

Существует конечный набор точек , такой что

Выберем так, что ,

Тогда при , существует из выбранного нами конечного набора, что , поэтому

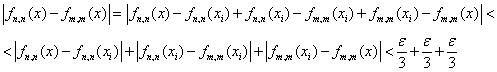
А это значит, что последовательность сходится, причём равномерно.

Замечание. В формулировке можно потребовать поточечную ограниченность, и доказать равномерную ограниченность.

Теорема. Если ядро непрерывно при , , то оператор Фредгольма является вполненепрерывным.

Доказательство.

В силу неравенства Коши-Буниковского

Если , то где

То есть последовательность равномерно ограничена, покажем, что она равностепенно непрерывна.

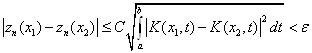
Как только , а последнее неравенство выполнено в силу непрерывности при .

В силу теоремы Арцела из последовательности можно выбрать равномерно сходящуюся подпоследовательность пределом которой будет непрерывная функция, из равномерной сходимости следует содимость в среднем а следовательно . Таким образом доказано существование элмента и существование сходящийся к нему подпоследовательности.

Определение. Симметричным оператором называется оператор

.

Теорема. Оператор Фредгольма является симметричным, если .

< Предыдущая		Следующая >