11. Неоднородное уравнение Фредгольма II-го рода.
Случай симметричного ядра.
Рассмотрим интегральное уравнение
-непрерывная функция, 
-непрерывное симметричное ядро.
Предположим, что решение этого уравнения существует.
Тогда для функции 
, справедлива теорема Гильберта-Шмидта, т. е 
, 
- собственные функции ядра, в сумме может быть и конечное число слагаемых. Используя тот факт, что
Получим, что 
. Таким образом, если решение существует, то оно представимо в виде: 
(1), где 
определяется соотношением: 
, т. е
(2)
1. 
. Когда ядро не вырождено, то с. ф. бесконечно много, покажем, что ряд сходится равномерно. В этом случае 
, а, следовательно, для достаточно больших 
,
Т. е. по т. Г-Ш ряд 
ряд сходится абсолютноя, а следовательно ряд из модулей является мажорирующим для ряда 
. Т. е. ряд (1) сходится абсолютно и равномерно.
Мы получили решение в предположении, что оно существует. Теперь проверим, что это выражение действительно является решением. В силу равномерной сходимости ряда его можно интегрировать почленно, тогда
,
Что и требовалось.
Пусть имеется два решения, тогда их разность удовлетворяет однородному интегральному уравнению 
, но 
не совпадает не с одним из с. з т. е 
.
Резольвента.
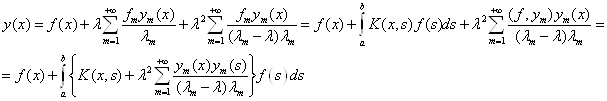Т. е 
, где 
2. Рассмотрим случай 
. Пусть 
-с. ф. ядра соответсвующие 
Если 
, то (2) противоречиво, пусть 
, тогда 
не определены остальные определены однозначно, т. е
(3)
То что это выражение определяет решение интегрального уравнения показывается аналогично случаю 1.
Таким образом доказана
Теорема. Пусть 
удовлетворяет указанным выше требованиям.
Если не совпадает ни с одни с. з ядра, то решение интегрального уравнения существует, единственно и представимо в виде (2).
Если и 
ортогональна всем с. ф., соответствующим , то решение существует, но не единственно и представимо в виде (3).
Если и не ортогональна хотя бы одной с. ф, то решения не существует.
Случай «малого» .
Откажемся от требования симметрии
Теорема. Если 
, решение существует и единственно и может быть найдено как предел равномерно сходящейся последовательности приближений 
.
Где 
- произвольная непрерывная функция.
Доказательство. Используем принцип сжатых отображений. Будем действовать в полном метрическом пространстве 
, где 
. Рассмотрим оператор
, Оператор 
действует из в , кроме того 
.
Т. к 
, то имеет место принцип сжатых отображений.
Резольвента.
Но 
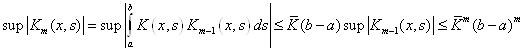
Т. е ряд 
сходится равномерно при
А значит можно перейти к пределу и поменять интегрирование и суммирование.
Это выражение переходит в случае симметричного ядра в то, что мы получили ранее.
Замечание. Эти результаты обобщаются на случай полярных ядер.
Замечание. Ограничение на можно ослабить.
Случай уравнения Вольтера
Теорема. Задача имеет единственное решение при любом .
, 
Пусть 
, тогда
,
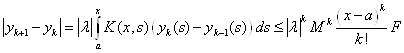. Т. о члены ряда мажорируются абсолютно сходящимся числовым рядом, что гарантирует равномерную сходимость.
Теоремы Фредгольма. Сформулируем теоремы для несимметричных ядер, обобщающие результаты полученные для симметричного ядра.
Интегральные уравнения
и 
Называются союзными.
Теорема. Собственные числа ядер и 
совпадают
Теорема. Пусть не является собственным значением ядра . Тогда решение интегрального уравнения и решение союзного уравнения существуют и единственны при любых и 
.
Теорема. Если является собственным значением ядра то однородное уравнение и союзное с ним однородное уравнение имеет одинаковое число линейно независимых собственных функций.
Теорема. Если является собственным значение ядра , то для существования решения неоднородного необходимо и достаточно, чтобы функция была ортогональна всем собственным функциям союзного ядра, отвечающему тому же .
Из второй и четвёртой теоремы следует альтернатива Фредгольма.
Альтернатива Фредгольма.
Либо интегральное уравнение имеет единственное решение при любой функции , либо существует нетривиальное решение союзного однородного уравнения.
Замечание. Теоремы Фредгольма обобщаются на случай полярных ядер.
| < Предыдущая | Следующая > |
|---|
