06. Линейные операторы

Линейным оператором, действующим из линейного пространства H в линейное пространство H1 , называется отображение, удовлетворяющее условиям:

Примеры линейных операторов

1. Определим , : , его линейность очевидна, оператор называется единичным.

2. В гильбертовом пространстве L2([A,B]) определим оператор, сопоставляющий функции , новую функцию

Множество линейных операторов действующее из в образуют линейное пространство.

Определение. Оператор непрерывен в точке X0, если из следует .

Оператор называется непрерывным, если он непрерывен в каждой точке.

Множество называется ограниченным, если оно содержится в шаре некоторого радиуса.

Оператор называется ограниченным, если всякое ограниченное в множество он переводит в ограниченное в

Теорема Если оператор линеен, то следующие утверждения эквивалентны.

1.  Существует точка , в которой оператор непрерывен.

2.  Оператор непрерывен.

3.  Оператор ограничен.

4.  Величина конечна

Доказательство. 1: Допустим непрерывен в докажем, что непрерывен в любой другой точке . , тогда для , что доказывает непрерывность оператора .

. Поскольку непрерывен, то он непрерывен и в нуле. Следовательно, , что для , справедливо . Пусть теперь X -- ограниченное множество в H, т. е. такое множество, что существует положительное число , . Пусть , .

Поскольку ограничен, то , откуда существование очевидна.

Пусть , тогда положим , , 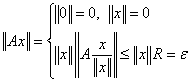т. е непрерывен в нуле.

< Предыдущая		Следующая >