05. Неравенство Минковского

Пусть , , тогда

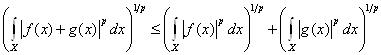
Доказательство. Для , оно очевидно, пусть , тогда

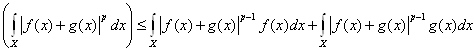
Применяя неравенство Гёльдера.

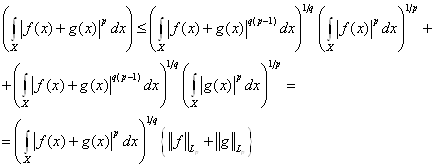
Здесь было использовано

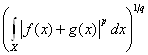Получим

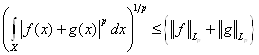
Для любого является нормированным пространством (неравенство треугольника выполняется в силу неравенства Минковского). При этом функции считаются равными, если они эквивалентны

Теорема. Для линейное нормированное пространство является полным, т. е. любая фундаментальная последовательность сходится к некоторой функции из .

Теорема. Для линейное нормированное пространство является сепарабельным.

Пусть измеримая функция на множестве . Говорят, что функция имеет конечный существенный максимум, если существует число такое, что . При этом существенным максимумом функции называется .

< Предыдущая		Следующая >