03. Линейные пространства.

Определение линейного пространства. Непустое множество любой природы называется линейным пространством, если выполнены следующие три условия.

1. На множестве определена операция сложения элементов. То есть Для любых двух элементов однозначно определен третий элемент , который называется суммой и обозначается: .

2. Для элементов множества определена операция умножения на число. Т. е. каждому элементу и каждому элементу некоторого числового поля поставлен в соответствие определённый элемент , который называется произведением элемента на число .

3. Указанные операции удовлетворяют следующим требованиям (аксиомам линейного пространства).

1). (коммутативность).

2). (ассоциативность)

3). , (существование нуля)

4) (существование противоположного элемента)

Эти четыре свойства можно было высказать короче: в L введена операция сложения, превращающая L в абелеву группу

5).

Аксиомы связывающие обе операции

Примеры линейных пространств.

2. Пространство непрерывных функций.

3. Пространство быстро убывающих функций.

4. Пространство , элементы которого последовательности , удовлетворяющие условию , с операциями , тот факт, что сумма двух последовательностей также принадлежит , следует из

Конечный набор элементов ., если существуют такие числа не все равные нулю . В противном случае элементы называются линейно независимыми.

Бесконечная система элементов пространства L называется Линейно независимой, если любая ее конечная подсистема линейно независима.

Нормированные пространства.

Метрическим пространством называется пара , состоящая из некоторого множества (пространства) элементов (точек) и расстояния, т. е. однозначной, неотрицательной, действительной функции , определённой для любых и подчиненной трём аксиомам.

Определение. Последовательность элементов в метрическом пространстве называется сходящейся в себе, если .

Определение. Метрическое пространство называется полным, если всякая фундаментальная последовательность имеет предел, принадлежащий этому пространству.

Теорема. (о вложенных шарах). Пусть в полном метрическом пространстве дана последовательность замкнутых шаров , вложенных друг в друга при , радиусы которых стремятся к нулю. Тогда существует одна и только одна точка , принадлежащая этим шарам.

Доказательство. По условию при , т. к. при , следовательно , т. е. последовательность фундаментальна. В следствии полноты существует . Докажем, что . Т. к , и и поскольку замкнут, то . Если бы существовала другая точка принадлежащая всем шарам, то , противоречие.

Нормой в линейном пространстве L называется функционал [т. е. отображение , удовлетворяющий следующим условиям:

1. Причём (положительная определённость нормы)

2. (неравенство треугольника)

Примеры норм.

1. 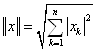В или .

2. в том же или .

5. Норма в

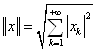
Сходимость в нормированном пространстве

Говорят, что , если

Определение. Множество называется Замкнутым, если оно совпадает со своим замыканием. Другими словами, множество M замкнуто, если из того, что последовательность точек Xn множества M сходится к точке X следует, что X принадлежит M.

Определение. Множество называется Плотным, если его замыкание совпадает со всем пространством.

Определение. Пространство называется Сепарабельным, если в нем существует плотное счетное подмножество.

Пример незамкнутого подпространства. Подпространство пространства , состоящее из всех многочленов, незамкнуто.

В самом деле, пусть .Согласно формуле Тейлора с остаточным членом в форме Лагранжа можем записать

Окончательно получаем, что последовательность Pn лежит в подпространстве многочленов, сходится (к функции
), но предельная функция не лежит в пространстве многочленов. Следовательно, рассматриваемое подпространство незамкнуто.

Последовательность точек Xn нормированного линейного пространства L называется Фундаментальной, если для любого существует номер N0 такой, что для всех M,N>N0 выполняется неравенство .

Определение. Линейное нормированное пространство L называют Полным, если всякая его фундаментальная последовательность сходится.

Определение. Полное линейное нормированное пространство называется Банаховым.

Примеры.

1) , ,- пространство числовых последовательностей, для которых с нормой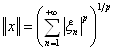

2) Пространство ограниченных числовых последовательностей с нормой

3) - пространство непрерывных на функций .

< Предыдущая		Следующая >