2. Ряды. Сумма числового ряда. Сходимость

Конечные суммы называются частичными суммами ряда

. (2.1.1)

Числовой ряд (2.1.1) называется сходящимся, если сходится последовательность его частичных сумм . Предел последовательности частичных сумм называется суммой ряда .

Пример 2.1.1. Исследовать сходимость геометрической прогрессии:

.

Решение. Пусть обозначает -ую частичную сумму геометрической прогрессии, т. е. .

Следовательно, .

Отсюда и для частичной суммы геометрической прогрессии справедливо равенство:

.

Находим

Из определения сходящегося ряда следует, что геометрическая прогрессия сходится тогда и только тогда, когда и ее сумма, в этом случае, равна.

Ответ: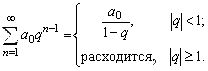

Пример 2.1.2. Исследовать сходимость ряда .

Решение. Данный ряд - геометрическая прогрессия, знаменатель которой

.

Следовательно, как следует из примера (2.1.1) сходится.

Ответ: сходится.

< Предыдущая		Следующая >