1.5. Интеграл от функции комплексной переменной

Пусть дуга направленной кусочно-гладкой кривой задана параметрическим уравнением . Пусть - начальная точка и - конечная точка дуги. Тогда

.

Пример 1.5.1. Вычислить , где - отрезок прямой от точки До точки .

Решение. Параметрическое задание отрезка: с . Отсюда , .

.

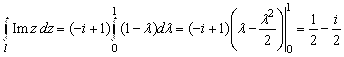Ответ: .

Пример 1.5.2. Вычислить , где - любое целое число.

Решение. Поскольку дуга – это окружность, целесообразно следующее параметрическое задание , .

Поэтому

Так как , то окончательно получим

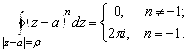
Ответ: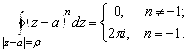

Замечание. Значение интеграла не зависит от .

Если функция Является аналитической в области, где расположена дуга , то существует первообразная функции, т. е.. В этом случае справедлива Формула Ньютона - Лейбница

, где , - начальная и конечная точки дуги соответственно.

Пример 1.5.3. Вычислить , где - отрезок прямой от точки До точки .

Решение. Функция является аналитической функцией с первообразной . Поэтому воспользуемся формулой Ньютона - Лейбница

.

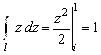Ответ: .

Теорема Коши для односвязной области. Если - аналитическая функция в односвязной области , а - замкнутый контур в , то .

Пример 1.5.4. Вычислить .

Решение. Заметим, что функция - аналитическая на всей комплексной плоскости. Поэтому в силу теоремы Коши для односвязной области этот интеграл равен нулю.

Ответ: .

Интегральная формула Коши для односвязной области

Пусть - аналитическая функция в односвязной области . Пусть точка , - простой замкнутый контур в , охватывающий точку . Тогда

.

Пример 1.5.5. Вычислить интеграл .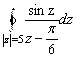

Решение. Функция - аналитическая на всей комплексной плоскости. Поэтому по интегральной формуле Коши интеграл равен .

Ответ: .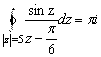

< Предыдущая		Следующая >