2.10. Степенные ряды

Теорема Абеля. Если степенной ряд сходится в точке , то он абсолютно сходится для всех , таких, что , причем сходимость будет равномерной в любом замкнутом круге . Если же ряд расходится в точке , то он расходится и для всех таких, что .

Замечание. а) Из теоремы Абеля следует существование круга сходимости.

Б) Из признака Вейерштрасса следует: если степенной ряд абсолютно сходится и на границе круга сходимости, то сходимость равномерная внутри всего замкнутого круга сходимости.

Пример 2.11.1. Найти область абсолютной сходимости и область равномерной сходимости ряда .

Решение. Выполним замену переменной . Тогда ряд примет вид

.

Составим ряд из модулей , к которому применим признак Даламбера. Для этого найдем

.

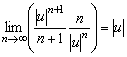По признаку Даламбера ряд абсолютно сходится, если . Отсюда радиус сходимости степенного ряда равен . Исследуем абсолютную сходимость на границе круга сходимости. Если , то ряд - это гармонический ряд , который, как известно, расходится. Поэтому по теореме Абеля ряд равномерно сходится . Возвращаясь к исходной переменной, запишем ответ.

Ответ: абсолютно сходится, равномерно сходится.

Пример 2.11.2. Найти область абсолютной сходимости и область равномерной сходимости ряда .

Решение. Выполним замену переменной . Тогда ряд примет вид

.

Составим ряд из модулей , к которому применим признак Даламбера. Для этого найдем

.

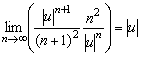По признаку Даламбера ряд абсолютно сходится, если . Отсюда радиус сходимости степенного ряда равен . Исследуем абсолютную сходимость на границе круга сходимости. Если , то ряд - это сходящийся ряд Дирихле . Поэтому по признаку Вейерштрасса ряд равномерно сходится . Возвращаясь к исходной переменной, запишем ответ.

Ответ: Абсолютно и равномерно сходится.

< Предыдущая		Следующая >