2.09. Равномерная сходимость функционального ряда. Признак Вейерштрасса

Сходящийся в области функциональный ряд называется Равномерно сходящимся в этой области, если для  любого найдется число такое, что для остатка функционального ряда при всех и  одновременно имеет место оценка .

Признак Вейерштрасса. Пусть функциональный ряд сходится области и пусть существует сходящийся знакоположительный числовой ряд такой, что для всех и для всех , начиная с некоторого номера, члены ряда удовлетворяют условию . Тогда ряд сходится абсолютно и равномерно в области .

Пример 2.10.1. Исследовать абсолютную и равномерную сходимость по признаку Вейерштрасса .

Решение. При ряд сходится. Поэтому, без ограничения общности можно предполагать, что . Тогда сходимость ряда равносильна сходимости ряда .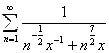

Так как

, то при или Достигается минимум для знаменателя, а, следовательно, максимум для дроби. Поэтому

.

Ряд сходится как ряд Дирихле с показателем степени . Отсюда исходный ряд сходится абсолютно и равномерно по признаку Вейерштрасса при всех значениях переменной.

Ответ: сходится абсолютно и равномерно при всех .

< Предыдущая		Следующая >