2.08. Условная сходимость. Признак Абеля - Дирихле

Абсолютная сходимость числового ряда. Если ряд из модулей сходится, то исходный ряд называется абсолютно сходящимся.

Условная сходимость числового ряда. Если ряд сходится, а ряд из модулей расходится, то исходный ряд называется условно сходящимся.

Пример 2.9.1. Исследовать сходимость ряда .

Решение. Для исследования абсолютной сходимости рассмотрим ряд . Как известно (пример 2.7.2), гармонический ряд расходится. Поэтому у исходного ряда нет абсолютной сходимости. Однако как показано в примере 2.8.1 исходный ряд удовлетворяет предположениям теоремы Лейбница. Поэтому ряд Сходится.

Ответ: Сходится условно.

Для проверки условной сходимости, помимо признака Лейбница, применяются также следующий признак:

Признак Абеля - Дирихле. Пусть дан ряд , в котором последовательность монотонно стремится к , а последовательность частичных сумм ряда равномерно ограничена, тогда ряд - сходится.

Пример 2.9.2. Для произвольно заданного вещественного числа доказать равномерную ограниченность последовательности частичных сумм ряда .

Решение. Заметим, что . Поэтому для частичной суммы имеет место равенство

.

Как показано в примере 2.1.1 для частичной суммы геометрической прогрессии (независимо от знаменателя) справедливо равенство:

.

Поэтому

.Следовательно,

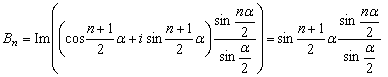. Отсюда

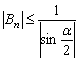при всех .

Ответ: .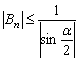

Пример 2.9.3. Для произвольно заданного вещественного числа доказать равномерную ограниченность последовательности частичных сумм ряда .

Решение. Заметим, что . Поэтому для частичной суммы имеет место равенство

.

Также как в примере 2.9.2 запишем частичную сумму геометрической прогрессии по формуле:

.

Отсюда

.Следовательно,

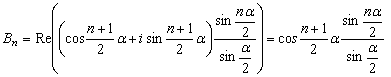. Отсюда

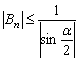при всех .

Ответ: .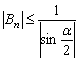

Пример 2.9.4. Исследовать сходимость ряда .

Решение. Как показано в примере 2.4.1 ряд расходится. Поэтому расходится ряд .

Отсюда нет абсолютной сходимости у ряда . Исследуем условную сходимость по признаку Абеля - Дирихле. Как показано в примере 2.9.2, частичные суммы ряда равномерно ограничены числом . Кроме того, последовательность монотонно стремится к . Следовательно, ряд сходится по признаку Абеля - Дирихле.

Ответ: сходится условно.

< Предыдущая		Следующая >