2.07. Знакочередующиеся ряды. Признак Лейбница. Оценка остатка ряда

Теорема Лейбница. Если и для всех , то знакочередующийся ряд

сходится. При этом для всех - модуль -ого остатка ряда не превышает модуля следующего члена ряда.

Пример 2.8.1. Проверить выполнение условий теоремы Лейбница для ряда . В случае положительного ответа оценить.

Решение. Вычисляем . Кроме того, последовательность монотонно убывает. Следовательно, все предположения теоремы Лейбница выполнены. Поэтому справедлива оценка остатка ряда по модулю

.

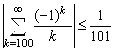Ответ: удовлетворяет предположениям теоремы Лейбница. .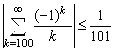

< Предыдущая		Следующая >