2.06. Интегральный признак Коши

Если функция и (монотонно убывает) при всех , то ряд сходится тогда и только тогда, когда сходится несобственный интеграл .

Пример 2.7.1. Исследовать по интегральному признаку сходимость ряда Дирихле.

Решение. Рядом Дирихле называется ряд вида . Так как при всех и , то исследуем сходимость по интегральному признаку сходимости. Вычисляем

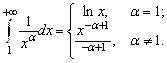
Отсюда

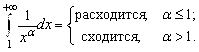
Соответственно,

Ответ: ряд

Ряд Дирихле сходится, если и расходится, если .

Пример 2.7.2. Исследовать сходимость гармонического ряда .

Решение. Гармонический ряд - это частный случай ряда Дирихле с . Поэтому ряд расходится.

Ответ: расходится.

Пример 2.7.3. Исследовать сходимость ряда .

Решение. Ряд - это частный случай ряда Дирихле с . Поэтому ряд сходится.

Ответ: Сходится.

< Предыдущая		Следующая >