2.05. Признак Коши абсолютной сходимости рядов
Признак Коши (радикальный). Пусть ![]() — ряд с неотрицательными членами
— ряд с неотрицательными членами ![]() и
и ![]() , тогда
, тогда
1) в случае ![]() ряд
ряд ![]() сходится,
сходится,
2) в случае ![]() ряд
ряд ![]() расходится и не выполнено необходимое условие сходимости,
расходится и не выполнено необходимое условие сходимости,
3) в случае ![]() вопрос остается открытым.
вопрос остается открытым.
Пример 2.6.1. Исследовать сходимость ряда ![]() .
.
Решение. Для применения признака Коши преобразуем модуль
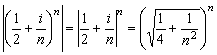 .
.
Отсюда
 .
.
Поэтому по признаку Коши ряд сходится абсолютно.
Ответ: ![]() Сходится абсолютно.
Сходится абсолютно.
Пример 2.6.2. Исследовать сходимость ряда ![]() .
.
Решение. Для применения признака Коши преобразуем модуль
 .
.
Отсюда
 .
.
Поэтому по признаку Коши не выполнено необходимое условие сходимости, а, следовательно, ряд расходится.
Ответ: ![]() Расходится.
Расходится.
| < Предыдущая | Следующая > |
|---|