37. Ряд Лорана

1. Кольцо сходимости ряда Лорана.

Определение. Рядом Лорана называется степенной ряд вида (суммирование ведется и по положительным, и по отрицательным степеням), здесь Z0 – фиксированная точка комплексной плоскости.

Второе слагаемое называется Правильной (регулярной) частью ряда Лорана, первое - Главной частью ряда Лорана.

Очевидно, областью сходимости ряда Лорана будет пересечение областей сходимости его регулярной и главной части.

Из теоремы Абеля следует, что регулярная часть сходится в круге и является в нем аналитической функцией. Î C¥(|Z-Z0|<R1).

Сделаем замену 1/(Z-Z0)=x; главная часть ряда Лорана принимает вид . По теореме Абеля такой ряд сходится при , что соответствует внешности круга .

При R2<R1 существует общая область сходимости - Круговое кольцо R2<|Z-z0|<R1.
Свойства степенного ряда, следующие из теоремы Абеля :

1. ÎC¥(R2<|Z-Z0|<R1).

2. Внутри кругового кольца сходимости ряд Лорана можно почленно дифференцировать и интегрировать любое число раз, при этом полученные ряды также аналитичны в том же кольце.

3. R1 определяется через {CN}, N=0,1,2...,: R1=1/L1, L1= или L1=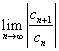 , а R2 - через {c-n}, n=1,2...,: R2=, или R2=.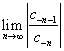

4. Коэффициенты ряда Лорана CN через значения суммы ряда в точке Z0 не определяются! В точке Z0 Сумма ряда Лорана не определена!

Пимеры:

1) ,

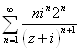2) ,

3) ,

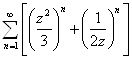< Предыдущая		Следующая >