38. Теорема о разложении функции комплексной переменной, аналитической в круговом кольце в ряд Лорана
Теорема (Теорема Лорана) Если F(z)ÎC¥(R2<|Z-Z0|<R1), то она однозначно разложима в этом кольце в ряд Лорана F(z)= ![]() .
.
Доказательство. Фиксируем произвольную точку Z внутри кольца: (R2<|z-z0|<R1) и построим окружности C1 :|x-Z0|=R'1 и C2 : |x-z0|=R'2 , с центром в точке Z0 и радиусами R'1 и R'2 : R2<R'2<|z-z0|<R'1<R1.
По Формуле Коши для многосвязной области в силу аналитичности F(z), справедливо
F(z)=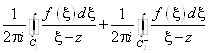 =F1(Z)+F2(Z)
=F1(Z)+F2(Z)
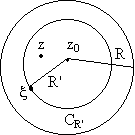
На окружности C1 :|x-Z0|=R'1 выполняется неравенство 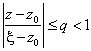 . Поэтому, дробь 1/(x-Z) можно представить в виде
. Поэтому, дробь 1/(x-Z) можно представить в виде
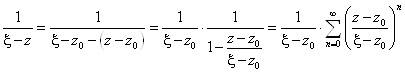
Проведя почленное интегрирование, что возможно в силу равномерной сходимости ряда по переменной x на C1
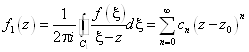 ,
,
Где введено обозначение
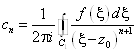 , N>0.
, N>0.
На окружности C2:|x-z0|=R'2 выполняется неравенство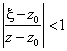 . Поэтому, дробь
. Поэтому, дробь
1/(x-Z) можно представить в виде
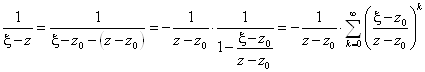
В результате почленного интегрирования этого ряда получим:
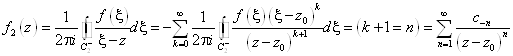 ,
,
Где введено обозначение ![]()
Изменив направление интегрирования, получим:
![]() , N>0
, N>0
Подынтегральные функции в выражениях для Cn и C-n являются аналитическими в круговом кольце R2<|z-z0|<R1.. Поэтому в силу Теоремы Коши значения соответствующих интегралов не изменится при произвольной деформации контуров интегрирования в области аналитичности подынтегральных функций. Это позволяет записать общее выражение
![]() , N=0,±1,±2,…
, N=0,±1,±2,…
Где C - произвольный замкнутый контур, лежащий в кольце R2<|z-z0|<R1 и содержащий точку Z0 внутри. Для F(z) окончательно можно записать:
F(z)= .
.
Т. к. Z - произвольная точка внутри кольца R2<|z-z0|<R1 Þ ряд ![]() сходится к F(z) всюду внутри данного кольца, причем в замкнутом кольце R2<R'2£|z-z0|£R'1<R1 ряд сходится к F(z) Равномерно.
сходится к F(z) всюду внутри данного кольца, причем в замкнутом кольце R2<R'2£|z-z0|£R'1<R1 ряд сходится к F(z) Равномерно.
Докажем единственность разложения в ряд Лорана. Предположим, что имеет место другое разложение F(z)= ![]() , где хотя бы один коэффициент C'n¹Cn. Тогда всюду внутри кольца R2<|z-z0|<R1 имеет место равенство:
, где хотя бы один коэффициент C'n¹Cn. Тогда всюду внутри кольца R2<|z-z0|<R1 имеет место равенство: ![]() =
=![]()
Проведем окружность CR , радиуса R: R 2<R<R1 , с центром в точке Z0 . Тогда ряды ![]() И
И ![]() Сходятся на CR Равномерно.
Сходятся на CR Равномерно.
Умножим оба ряда на (z-z0)-M-1 , где M- произвольное целое число и проинтегрируем почленно по окружности CR.
Рассмотрим 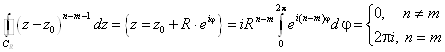 .
.
Т. о. для " M C'm=cm.
Примеры. Разложить в ряд Лорана с центром в ![]()
1) ![]() ,
, ![]()
2) ![]() ,
, ![]()
| < Предыдущая | Следующая > |
|---|