36. Теорема единственности определенной аналитической функции

Теорема 22.1. Если F1 (Z) и F 2(Z) ÎC¥(g) и $ {ZN}®AÎg, (Zi¹Zk) и F1(ZN)=F2(ZN ), то F1(Z)ºF2 (Z) для " ZÎg.
Для доказательства достаточно при помощи теоремы о нулях установить, что функция H(Z)=F1(Z)-F2(Z)º0 в g.

Следствия теоремы единственности.

В области g Может существовать Только одна аналитическая функция, принимающая заданные значения на

a) {ZN}®AÎg, (Zi¹Zk) сходящейся последовательности различных точек.

B ) xÎgÌ g, кусочно-гладкой кривой g.

C) "ZÎg'Ìg в произвольной подобласти области g.

Т. е. с этих множеств функцию F(Z) можно аналитически продолжить, причем единственным способом.

На этом факте основано продолжение элементарных функций с действительной оси. В самом начале курса мы формально вели элементарные функции комплексного переменного (expZ, sinZ, cosZ…) совпадение обозначений которых с функциями, заданными на действительной оси могло оказаться чистой случайностью.

Однако мы получили разложения в степенные ряды функций комплексного переменного

,

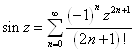
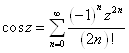
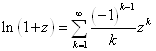
Эти ряды на действительной оси Z=x совпадают с рядами Тейлора для элементарных функций действительного переменного, полученными в курсе анализа функций действительных переменных. Т. о. элементарные функции комплексного переменного совпадают со своими аналогами на действительной оси (или отрезках действительной оси). Поэтому мы можем утверждать, что их аналитическое продолжение на комплексную плоскость единственно, согласно теореме единственности (случай b – функции совпадают на кусочно-гладкой кривой).

Продолжение соотношений типа c действительной оси также единственно, как продолжение функции .

Теорема 22.2. На границе круга сходимости степенного ряда лежит хотя бы одна особая точка аналитической функции .

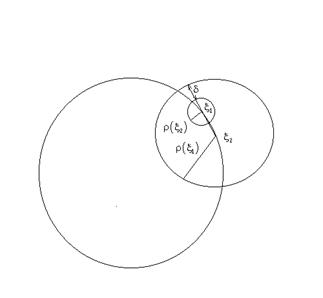
Доказательство (От противного) Если бы все точки границы были бы правильными, то "x: |x-Z0|=R- граница круга сходимости $r(x)>0: "Z |x-Z|<r(x), т. е. задана строго положительная функция r(x) Докажем, что для этой функции в любых двух точках границы круга сходимости выполнено неравенство: .

Предположив, что это неравенство не выполнено, получим, например,

,

Но тогда круг лежит целиком внутри круга

Тогда степенные ряды с центром разложения в точках и совпадают в общей части кругов сходимости и и т. о. в силу единственности аналитического продолжения радиус круга сходимости ряда больше, чем . Это противоречие и доказывает неравенство

.

Т. о. вещественнозначная функция - равномерно непрерывна на окружности |x-Z0|=R, и в силу ограниченности достигает своей нижней грани. Т. е. $x0: , т. е. $x0 - особая точка на границе круга сходимости.

Заметим, что часть этого круга лежит вне круга сходимости исходного степенного ряда.

Следствие. Радиус сходимости степенного ряды аналитической функции равен расстоянию от центра разложения до ближайшей особой точки. Это можно использовать для определения радиуса сходимости, например, ряды

Центр разложения z=0, ближайшая особая точка z=-1 – точка ветвления функции .

< Предыдущая		Следующая >