35. Единственность определения аналитической функции
1. Понятие правильной точки.
Пусть F(Z) задана в g, за исключением может быть некоторых изолированных точек.
Точка Z0Îg называется Правильной точкой функции F(Z), заданной в g, Если $ ![]() в круге |Z-z0|<r(Z0), где r(Z0)>0 - радиус сходимости степенного ряда.
в круге |Z-z0|<r(Z0), где r(Z0)>0 - радиус сходимости степенного ряда.
Все остальные точки ZÎg - Особые точки Функции F(Z), заданной в g.
Замечание. Если F(Z)ÎC¥ (g), то все ZÎg - Правильные Точки F(Z). Если F(Z) задана в ![]() , то граничные точки могут быть как правильными, так и особыми.
, то граничные точки могут быть как правильными, так и особыми.
2. Нули аналитической функции.
Определение. Пусть F(Z)ÎC¥(g); F(Z0)=0, Z0Îg, тогда Z0 - Нуль аналитической функции. ![]() Þ С0 =0. В этом случае
Þ С0 =0. В этом случае ![]()
Если C1=…= CN-1 =0, а CN¹0, то Z0 - Нуль n-того порядка. В этом случае ![]()
Заметим, что в нуле N-того порядка F(Z0) = F ' (Z0)=… = F(n-1)(Z0) = 0, F(n)(Z0)¹0 и F(Z)=(Z-Z0)N×F1(Z), где F1(Z0) ¹0.
Если Cn=0 "N, то F(z)º0.
Примеры.
1) ![]() Точка Z=0 - нуль первого порядка.
Точка Z=0 - нуль первого порядка.
2) 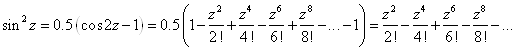 Точка Z=0 - нуль второго порядка.
Точка Z=0 - нуль второго порядка.
3) ![]() Точка
Точка ![]() - ноль третьего порядка
- ноль третьего порядка
4) ![]() Точка
Точка ![]() - ноль второго порядка
- ноль второго порядка
Теорема о нулях аналитической функции.
Пусть F(Z)ÎC¥(g) и $ ![]() : (Zi¹Zk , все ZNÎg и F(ZN)=0), имеющем предельную точку (точку сгущения) AÎg (
: (Zi¹Zk , все ZNÎg и F(ZN)=0), имеющем предельную точку (точку сгущения) AÎg (![]() ZN=AÎg). Тогда F(Z)º0, для "ZÎg.
ZN=AÎg). Тогда F(Z)º0, для "ZÎg.
Доказательство.
Т. к. AÎg, то ![]() , причем радиус сходимости этого степенного ряда R0 не меньше расстояния от A до ¶g.
, причем радиус сходимости этого степенного ряда R0 не меньше расстояния от A до ¶g. 
F(Z)ÎC¥(g)=> по непрерывности F(a)=0 => С0=0, т. о.
![]()
![]()
Новая функция F1(Z) отличается от исходной одним множителем (z-a) => имеет те же нули![]() , что и F(z). По непрерывности F1(A)=0 => С1=0.
, что и F(z). По непрерывности F1(A)=0 => С1=0.
Продолжая в том же духе, получим Cn=0 "N. Это означает, что F(z)º0 "Z: |Z-a|<R0
Докажем, что F(Z1)º0, для "Z1Îg.
Соединим Z1 и A кусочно-гладкой кривой L, целиком лежащей в g и отстоящей от ее границы ¶g на расстояние D>0.
Поскольку "Z: |Z-a|<R0 можно рассматривать, как предел последовательности нулей F(z), то в качестве нового центра разложения можем выбрать точку Z=a1 – точку пересечения кривой L с окружностью |Z-a|=R0. Проведя аналогичные рассуждения, получим, что F(z)º0 "Z: |Z-a1|<R1, где R1³D. Продолжая рассуждать подобным образом, покроем всю кривую L кругами, внутри которых F(z)º0. При этом точка Z1 попадет внутрь последнего круга и тем самым F(z1)= 0.
Следствие. F(Z)ÎC¥(g) внутри любой замкнутой подобласти ![]() может иметь лишь конечное число нулей, иначе
может иметь лишь конечное число нулей, иначе ![]() .
.
Пример. sin (1/Z) )ÎC¥(g/0) имеет в конечной замкнутой области бесконечное число нулей {Zn=1/pN}®0. Что не противоречит теореме, т. к. в z=0 нарушается аналитичность.
| < Предыдущая | Следующая > |
|---|